ConnectSystemModelController[model,controller]
connects the system model model with a controller according to the controller data controller.




ConnectSystemModelController
ConnectSystemModelController[model,controller]
connects the system model model with a controller according to the controller data controller.
Details


- ConnectSystemModelController is typically used to connect a controller to a SystemModel plant model and give the closed-loop system back. The resulting system can then be simulated and analyzed for real-world performance.
- The model can be a SystemModel object, a full model name string or a shortened model name accepted by SystemModel.
- ConnectSystemModelController["NewModel",…] gives the created model the name "NewModel".
- The controller is a SystemsModelControllerData object produced by control design functions.
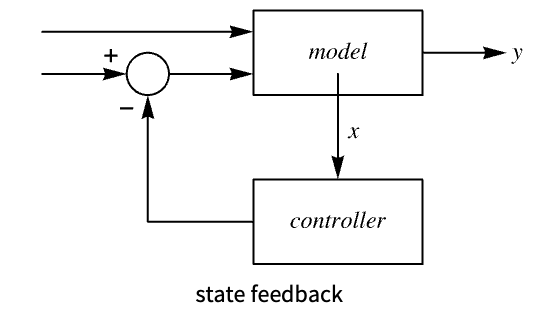
- With state feedback from model, the control design functions include:
-
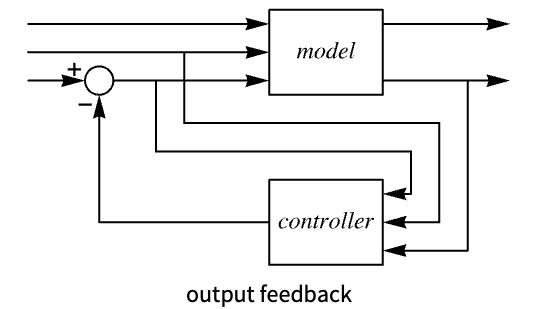
StateFeedbackGains pole placement state feedback LQRegulatorGains linear quadratic optimal control DiscreteLQRegulatorGains discrete-time linear quadratic optimal control ModelPredictiveController constrained model predictive controller - With output feedback from model, the controller design functions include:
-
EstimatorRegulator assembling state feedback and state estimator LQGRegulator linear quadratic control and estimator PIDTune automatically tuned PID controller - ConnectSystemModelController returns a SystemModel.
Examples
open all close allBasic Examples (1)
Scope (16)
StateFeedbackGains (3)
Start with a model for a submerging submarine:
Linearize it around an equilibrium point:
Generate the closed-loop system for the controlled model:
Perturb the submarine with a vertical force:
Simulate the closed-loop system with the same disturbance:
Plot the depth of the submarine in the original model:
In the closed-loop system, the submarine changes its density to preserve its depth:
Start with a model for a spacecraft in a circular orbit:
Linearize it around an equilibrium point:
Generate the closed-loop system for the controlled model:
Simulate the original model with an initial velocity:
Simulate the closed-loop system with the same initial velocity:
Plot the deviations from the circular trajectory in the original model:
The closed-loop system brings the spacecraft back to its circular orbit:
Start with a model for an inverted pendulum:
Linearize it around an equilibrium point:
Generate the closed-loop system for the controlled model:
Apply a tangential force to the pendulum and simulate it:
Simulate the closed-loop system with the same disturbance:
Plot the angle of the pendulum in the original model:
The closed-loop system applies a horizontal force and brings the pendulum back to the vertical position:
LQRegulatorGains (2)
Start with a model for a continuous stirred-tank reactor:
Linearize it around an equilibrium point:
Generate the closed-loop system:
Simulate the original model with a deficit in the concentration of the reactant from its equilibrium value:
Simulate the closed-loop system with the same initial condition:
Plot the change in reactant concentration in the original model:
The closed-loop system controls the flow rate and brings the concentration back to the equilibrium value:
Start with a model for a ball placed on top of a beam that can rotate around its center of mass:
Linearize it around an equilibrium point:
Generate the closed-loop system:
Simulate the original model placing the ball at the edge of the beam:
Simulate the closed-loop system with the same initial condition:
Plot the position of the ball, measured from the middle of the beam, in the original model:
The closed-loop system applies a torque and brings the ball back to the middle of the beam:
DiscreteLQRegulatorGains (2)
Start with a model for a continuous stirred-tank reactor:
Linearize it around an equilibrium point:
Generate the closed-loop system:
Simulate the original model with a deficit in the concentration of the reactant from its equilibrium value:
Simulate the closed-loop system with the same initial condition:
Plot the change in reactant concentration in the original model:
The closed-loop system controls the flow rate and brings the concentration back to the equilibrium value:
Start with a model for a ball placed on top of a beam that can rotate around its center of mass:
Linearize it around an equilibrium point:
Generate the closed-loop system:
Simulate the original model placing the ball at the edge of the beam:
Simulate the closed-loop system with the same initial condition:
Plot the position of the ball, measured from the middle of the beam, in the original model:
The closed-loop system applies a torque and brings the ball back to the middle of the beam:
EstimatorRegulator (2)
Start with a model for a spacecraft in a circular orbit:
Linearize it around an equilibrium point:
Design a controller and observer and put them together in EstimatorRegulator:
Generate the closed-loop system for the controlled model:
Simulate the closed-loop system with an initial velocity:
The closed-loop system brings the spacecraft back to its circular orbit:
Start with a model for an inverted pendulum:
Linearize it around an equilibrium point:
Design a controller and observer and put them together in EstimatorRegulator:
Generate the closed-loop system for the controlled model:
Simulate the closed-loop system with an initial angle away from the equilibrium:
The closed-loop system applies forces to bring the pendulum back to vertical position:
LQGRegulator (2)
Start with a model for a continuous stirred-tank reactor:
Linearize it around an equilibrium point:
Generate the closed-loop system for the controlled model:
Simulate the original model with a deficit in the concentration of the reactant from its equilibrium value:
The closed-loop system controls the flow rate and brings the concentration back to the equilibrium value:
Start with a model for a ball placed on top of a beam that can rotate around its center of mass and add some rotational damping:
Linearize it around an equilibrium point:
Generate the closed-loop system for the controlled model:
Simulate the closed-loop system placing the ball away from the middle of the beam:
The closed-loop system applies a torque and brings the ball back to the middle of the beam:
PIDTune (1)
ModelPredictiveController (2)
Start with a model for a camera stabilizer:
Linearize it around an equilibrium point:
Generate the closed-loop system for the controlled model:
Perturb the system with a vertical force:
Simulate the closed-loop system with the same disturbance:
Plot the position of the camera in the original model:
In the closed-loop system, the position of the camera does not change as much:
Start with a model for a continuous stirred-tank reactor:
Linearize it around an equilibrium point:
Generate the closed-loop system for the controlled model:
Simulate the original model with a deficit in the concentration of the reactant from its equilibrium value:
Simulate the closed-loop system with the same initial condition:
Plot the change in reactant concentration in the original model:
The closed-loop system controls the flow rate and brings the concentration back to the equilibrium value:
Tracking (2)
Start with a model for a submarine:
Linearize it around an equilibrium point:
Design a controller that tracks the depth of the submarine:
Generate the closed-loop system for the controlled model:
Simulate the closed-loop system providing a reference signal for the depth and noise:
Plot the reference and the output:
Plot the density change needed to reproduce the reference:
Start with a model for a ball placed on top of a beam that can rotate around its center of mass:
Linearize it around an equilibrium point:
Design a controller that tracks the position of the ball:
Generate the closed-loop system for the controlled model:
Simulate the closed-loop system providing a reference signal for the position and noise:
Related Guides
Related Links
Text
Wolfram Research (2021), ConnectSystemModelController, Wolfram Language function, https://reference.wolfram.com/language/ref/ConnectSystemModelController.html (updated 2022).
CMS
Wolfram Language. 2021. "ConnectSystemModelController." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/ConnectSystemModelController.html.
APA
Wolfram Language. (2021). ConnectSystemModelController. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ConnectSystemModelController.html
BibTeX
@misc{reference.wolfram_2025_connectsystemmodelcontroller, author="Wolfram Research", title="{ConnectSystemModelController}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/ConnectSystemModelController.html}", note=[Accessed: 21-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_connectsystemmodelcontroller, organization={Wolfram Research}, title={ConnectSystemModelController}, year={2022}, url={https://reference.wolfram.com/language/ref/ConnectSystemModelController.html}, note=[Accessed: 21-January-2026]}