ConvexHullMesh

ConvexHullMesh[{p1,p2,…}]

点 p1, p2, …からの凸包を表すBoundaryMeshRegionを与える．

ConvexHullMesh[mreg]

メッシュ領域 mreg の凸包を与える．

詳細とオプション

  • ConvexHullMeshは，凸包絡あるいは凸包としても知られている．
  • 凸包メッシュは，点を piを含む最小の凸集合である．
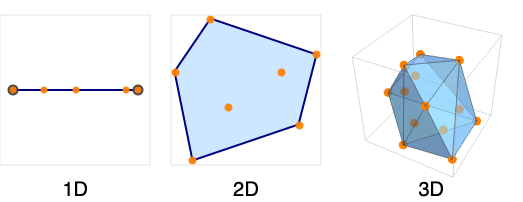
  • 凸包の境界は，1Dの点，2Dの線分，3Dの凸多角形からなる．
  • ConvexHullMeshはBoundaryMeshRegionと同じオプションを取る．

例題

すべて開くすべて閉じる

例  (3)

1D凸包メッシュ：

この領域は，点を含む最小の凸領域である：

2D凸包メッシュ：

この領域は，点を含む最小の凸領域である：

3D凸包メッシュ：

この領域は，点を含む最小の凸領域である：

スコープ  (3)

点集合から1D凸包メッシュを作る：

基本的な特性：

凸包メッシュは有界である：

凸包メッシュは全次元である：

面積と重心を求める：

点の帰属判定：

最近点とその距離を求める：

点集合から2D凸包メッシュを作る：

基本的な特性：

凸包メッシュは有界である：

凸包メッシュは全次元である：

その面積と重心を求める：

点の帰属判定：

最近点とその距離を求める：

点集合から3D凸包メッシュを作る：

基本的な特性：

凸包メッシュは有界である：

凸包メッシュは全次元である：

その体積と重心を求める：

その表面積を求める：

最近点とその距離を求める：

オプション  (13)

MeshCellHighlight  (3)

MeshCellHighlightを使ってConvexHullMeshの各部分をハイライトすることができる：

面を透過的にすることで，3DConvexHullMeshの内部構造を見ることができる：

個々のセルはセル指標を使ってハイライトすることができる：

セルそれ自体を使うこともできる：

MeshCellLabel  (2)

MeshCellLabelを使ってConvexHullMeshの各部分にラベルを付けることができる：

個々のセルにはセル指標を使ってラベルを付けることができる：

セルそれ自体を使うこともできる：

MeshCellMarker  (1)

MeshCellMarkerを使ってConvexHullMeshの各部分に値を割り当てることができる：

MeshCellLabelを使ってマーカーを示す：

MeshCellShapeFunction  (2)

MeshCellShapeFunctionを使ってConvexHullMeshの各部分についての関数を指定することができる：

個々のセルはセル指標を使って描くことができる：

セルそれ自体を使うこともできる：

MeshCellStyle  (3)

MeshCellStyleを使ってConvexHullMeshの各部分のスタイルを指定することができる：

面を透過的にすることで，3D ConvexHullMeshの内部構造を見ることができる：

個々のセルはセル指標を使ってハイライトすることができる：

セルそれ自体を使うこともできる：

PlotTheme  (2)

格子線と凡例のあるテーマを使う：

テーマを使ってワイヤーフレームを描く：

アプリケーション  (2)

5つの四面体を組み合せた凸包は十二面体である：

牛の凸包を計算する：

牛と凸包を可視化する：

特性と関係  (3)

ConvexHullMeshは，事実上，DelaunayMeshのBoundaryMeshである：

3Dで：

DelaunayMeshを使って，凸包内部のドロネー(Delaunay) 三角形分割を得る：

TriangulateMeshを使って内部の三角形分割を制御する：

考えられる問題  (1)

ConvexHullMeshは全次元のメッシュ領域しか返さない：

ConvexHullRegionを使って凸包を得る：

Wolfram Research (2014), ConvexHullMesh, Wolfram言語関数， https://reference.wolfram.com/language/ref/ConvexHullMesh.html （2020年に更新）.

テキスト

Wolfram Research (2014), ConvexHullMesh, Wolfram言語関数， https://reference.wolfram.com/language/ref/ConvexHullMesh.html （2020年に更新）.

CMS

Wolfram Language. 2014. "ConvexHullMesh." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/ConvexHullMesh.html.

APA

Wolfram Language. (2014). ConvexHullMesh. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ConvexHullMesh.html

BibTeX

@misc{reference.wolfram_2024_convexhullmesh, author="Wolfram Research", title="{ConvexHullMesh}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/ConvexHullMesh.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_convexhullmesh, organization={Wolfram Research}, title={ConvexHullMesh}, year={2020}, url={https://reference.wolfram.com/language/ref/ConvexHullMesh.html}, note=[Accessed: 21-November-2024 ]}