Cot

Cot[z]

给出 z 的余切.

更多信息

  • 数学函数，适宜于符号和数值运算.
  • Cot 的自变量是以弧度为单位的.（乘以 Degree 从度数转换)
  • .
  • Cos[z]/Sin[z] 自动转换为 Cot[z]. TrigFactorList[expr] 实现分解.
  • 对于某些特殊参数，Cot 自动运算出精确值.
  • Cot 可求任意数值精度的值.
  • Cot 自动逐项作用于列表的各个元素. »
  • Cot 可与 Interval 和 CenteredInterval 对象一起使用. »

背景

  • Cot 是余切函数，三角学中的基本函数之一. 它被定义为正切函数的倒数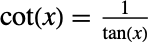：. 直角三角形中一个锐角 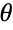的余切值在教科书上的等价定义是 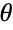角的邻直角边与对边长度的比值.
  • 当变量是 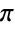的简单有理数倍时，Cot 会自动计算出精确值. 对一些更复杂的有理倍数，FunctionExpand 有时可用于算得显式的精确值. TrigFactorList 可将包含 Cot 的表达式因式分解为包含 Sin 和 Cos 的单项式. 若要使用角度值的变量，则可用符号 Degree 作为乘数（例如 Cot[30 Degree]）. 当给出精确数值表达式作为变量时，Cot 可以算出任意精度的数值结果. 对包含 Cot 的符号表达式，其他适用的操作运算有 TrigToExp、TrigExpand、Simplify 和 FullSimplify.
  • Cot 自动逐项作用于列表和矩阵. 相比之下，MatrixFunction 则可用于给出整个方阵的余切值（即用矩阵幂次代替普通幂次的余切函数的幂级数）而不是单个矩阵元素的余切值.
  • Cot 是周期函数，周期为 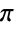，可由 FunctionPeriod 算出. Cot 满足恒等式 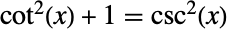，这其实与勾股定理等价. 余切函数的定义可由等式 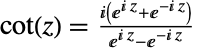扩展到复数变量 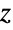上，其中 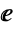是自然对数的底数. Cot 在 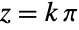且 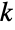是整数的这些点处取得极值 ComplexInfinity. Cot[z] 在原点处的级数展开为 sum_(k=0)^infty((-1)^k 2^(2 k) TemplateBox[{{2, , k}}, BernoulliB] )/((2 k)!)z^(2 k-1)，可由伯努利数 BernoulliB 构成的项表示.
  • Cot 的反函数是 ArcCot. 双曲余切函数是 Coth. 其他相关的数学函数有 Tan 和 Cos.

范例

打开所有单元关闭所有单元

基本范例  (6)

自变量以弧度为单位：

用 Degree 指定自变量以度为单位：

在一实数子集上绘图：

在复数的子集上绘图：

在 0级数展开：

奇点处的渐近展开式：

范围  (46)

数值计算  (6)

数值运算：

以高精度计算：

输出精度与输入精度相一致：

Cot 可接受复数：

在高精度条件下高效计算 Cot：

自动逐项计算数组中每个元素的值：

或用 MatrixFunction 计算矩阵形式的Cot 函数：

用 Interval 和 CenteredInterval 对象计算最坏情况下的区间：

或用 Around 计算一般情况下的统计区间：

特殊值   (5)

Cot 在固定点上的值：

无穷处的值：

Cot 的零点：

用 Solve 求 Cot 的零点：

替换结果：

可视化结果：

Cot 的奇点：

自动生成简单精确值：

更复杂的情形需要使用 FunctionExpand：

可视化  (3)

绘制 Cot 函数：

绘制 的实部：

绘制 的虚部：

，绘制极坐标图：

函数属性  (13)

Cot 的实定义域：

复定义域：

Cot 的值域是所有实数：

Cot 是周期为 的周期函数：

Cot 是一个奇函数：

Cot 具有镜像属性 cot(TemplateBox[{z}, Conjugate])=TemplateBox[{{cot, (, z, )}}, Conjugate]：

Cot 不是解析函数：

但是，它是亚纯函数：

Cot 在特定范围内是单调的：

Cot 不是单射函数：

Cot 是满射函数：

Cot 既不是非负，也不是非正：

在 π 的倍数处，Cot 有奇点和断点：

Cot 既不凸，也不凹：

TraditionalForm 格式：

微分  (3)

一阶导数：

高阶导数：

阶导数的公式：

积分  (3)

Cot 的不定积分：

Cot 在一个周期上的定积分：

更多积分：

级数展开式  (3)

使用 Series 求泰勒级数展开：

围绕 绘制 Cot 的前三个近似值：

Cot 级数展开式的通项:

Cot 可被应用于幂级数：

函数恒等式和化简  (6)

倍角的 Cot：

和的 Cot：

转换多倍角表达式：

将三角函数的和形式转换为积形式：

假定为实数变量 和 ，进行展开：

转换为复数指数：

函数表示  (4)

用 Tan 表示：

用 Jacobi 函数表示：

用 SphericalHarmonicY 表示：

用 Mathieu 函数表示：

应用  (4)

生成去除极点的图形：

在复平面生成图形：

余切函数将抛物线等角映射到单位圆盘中：

求解微分方程：

属性和关系  (12)

自动应用余切函数的基本奇偶性和周期性：

用 TrigFactorList 将 Cot 因式分解为 Sin 和 Cos：

包含三角函数的复杂表达式不会自动化简：

对参数进行假定的化简：

由反函数组成：

1 弧度是 度：

求解三角方程：

求解零点和极点：

求超越方程的数值根：

Cot 出现在许多数学方程的特例中：

计算符号余数和数值余数：

Cot 是一个数值函数：

可能存在的问题  (3)

机器精度输入不足以获得正确结果：

使用精确输入，得到正确结果：

需要增大 $MaxExtraPrecision 的值：

输出的精度可能比输入精度小得多：

巧妙范例  (6)

在整数点绘制 Cot：

连分数是高度正则化的：

Wolfram Research (1988)，Cot，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Cot.html （更新于 2021 年）.

文本

Wolfram Research (1988)，Cot，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Cot.html （更新于 2021 年）.

CMS

Wolfram 语言. 1988. "Cot." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2021. https://reference.wolfram.com/language/ref/Cot.html.

APA

Wolfram 语言. (1988). Cot. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Cot.html 年

BibTeX

@misc{reference.wolfram_2024_cot, author="Wolfram Research", title="{Cot}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/Cot.html}", note=[Accessed: 30-October-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_cot, organization={Wolfram Research}, title={Cot}, year={2021}, url={https://reference.wolfram.com/language/ref/Cot.html}, note=[Accessed: 30-October-2024 ]}