CriticalitySuccessImportance

CriticalitySuccessImportance[rdist,t]

時間 t におけるReliabilityDistribution rdist のすべての成分のクリティカリティ成功重要度を与える．

CriticalitySuccessImportance[fdist,t]

時間 t におけるFailureDistribution fdist のすべての成分のクリティカリティ成功重要度を与える．

詳細

  • CriticalitySuccessImportanceはクリティカリティ重要度因子としても知られている．
  • 成分 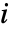のクリティカリティ成功重要度は，系が動いていると仮定して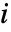， が系の成功に貢献している成分である確率である．
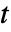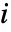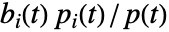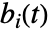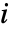  • 時間 における成分 のクリティカリティ成功重要度は で与えられる．ただし，は成分 のBirnbaum重要度であり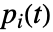， は成分 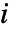が動いている確率であり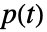， は系が動いている確率である．
  • 結果は rdist あるいは fdist における分布リストの成分順で返される．

例題

すべて開くすべて閉じる

例  (3)

異なる寿命分布を持ち，並列接続された2つの成分：

結果はReliabilityDistributionの分布リストと同じ順で与えられる：

連続成分のどちらも，系の稼働に貢献している：

故障の木に基づいたモデリングを使って系を定義する：

スコープ  (17)

ReliabilityDistributionモデル  (9)

等しい寿命分布を持ち，並列接続された2つの成分：

どちらの成分も動いている系に同じように貢献している：

等しい寿命分布を持ち，直列接続された2つの成分：

と は両方とも確率1で，直列の系の稼働に貢献している：

動くためには寿命分布が等しい3つの成分のうち2つが必要な系：

すべての成分が系の稼働に等しく貢献している：

寿命分布が等しい単純な混合系：

重要度を計算する：

成分 は常に系の稼働に貢献している：

1つの成分と並列で接続されている直列接続の系：

重要度を計算する：

成分 が系の稼働に最も貢献している：

単純な混合系でパラメータを変更することの効果を調べる：

重要度を計算する：

並列成分の1つである を悪化させることによる重要度の変化を示す：

分布が異なる2つの他の成分と並列の1つの成分：

時間のある1点での重要性尺度を厳密な結果として求める：

機械精度による結果：

記号式による結果：

任意の有効なReliabilityDistributionを使うことができる：

重要性尺度をプロットする：

部分系の重要性尺度を得るために段階を追って系をモデル化する：

重要度を時間に沿ってプロットする：

FailureDistributionモデル  (8)

2つの基本事象のどちらかが頂上事象に繋がる：

どちらの事象も頂上事象の発生防止に貢献している：

両方の基本事象が一緒になってはじめて頂上事象に至る：

両方の事象が同じように頂上事象に繋がる可能性がある：

基本事象の分布が等しいボーティングゲート：

ボーティングゲートの同一事象は故障を防ぐための確率が等しい：

AndゲートとOrゲートの両方がある単純な系：

クリティカリティ重要度を計算する：

頂上事象がまだ発生していない場合，事象 が最も頂上事象を防ぐ可能性がある：

AndゲートとOrゲートの両方がある単純な系：

重要度を示す：

頂上事象がまだ発生していない場合は，事象 は確率1でそれが発生していないことに貢献していない：

単純な混合系におけるパラメータの変更の効果を調べる：

重要度を計算する：

基本事象の1つである を悪化させた場合の重要度の変化を示す：

任意の有効なFailureDistributionを使うことができる：

重要性尺度をプロットする：

部分系の重要性尺度を得るために段階を追って系をモデル化する：

時間に沿って重要度をプロットする：

アプリケーション  (3)

作業時間が3時間のとき，どの成分が成功に最も貢献する可能性があるか求める：

時間に沿って重要度を示す：

作業時間が3時間のとき，成分 が系の成功に最も貢献する可能性がある：

1つの成分が直列で2つの成分が並列の系について調べる．クリティカリティ成功重要性尺度に照らしてどの成分が最も重要であるかを判断する：

成分 は系の成功に常に貢献する：

次の系を仮定する：

重要度を計算する：

すべての について，重要度の順序は であると言える：

特性と関係  (3)

CriticalitySuccessImportanceはProbabilityによって定義することができる：

すべての成分のBirnbaumImportance：

成分の信頼性を系の信頼性で割った成分の重み：

結果の成功に基づいたクリティカリティ重要度：

定義と比較する：

直列の系では，成功に基づいたクリティカリティ重要度はすべての成分について常に1である：

無関係な成分の重要度は0である：

Wolfram Research (2012), CriticalitySuccessImportance, Wolfram言語関数， https://reference.wolfram.com/language/ref/CriticalitySuccessImportance.html.

テキスト

Wolfram Research (2012), CriticalitySuccessImportance, Wolfram言語関数， https://reference.wolfram.com/language/ref/CriticalitySuccessImportance.html.

CMS

Wolfram Language. 2012. "CriticalitySuccessImportance." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CriticalitySuccessImportance.html.

APA

Wolfram Language. (2012). CriticalitySuccessImportance. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CriticalitySuccessImportance.html

BibTeX

@misc{reference.wolfram_2024_criticalitysuccessimportance, author="Wolfram Research", title="{CriticalitySuccessImportance}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/CriticalitySuccessImportance.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_criticalitysuccessimportance, organization={Wolfram Research}, title={CriticalitySuccessImportance}, year={2012}, url={https://reference.wolfram.com/language/ref/CriticalitySuccessImportance.html}, note=[Accessed: 21-November-2024 ]}