BarlowProschanImportance[rdist]
gives the Barlow–Proschan importances for all components in the ReliabilityDistribution rdist.
BarlowProschanImportance[fdist]
gives the Barlow–Proschan importances for all components in the FailureDistribution fdist.


BarlowProschanImportance
BarlowProschanImportance[rdist]
gives the Barlow–Proschan importances for all components in the ReliabilityDistribution rdist.
BarlowProschanImportance[fdist]
gives the Barlow–Proschan importances for all components in the FailureDistribution fdist.
Details
- The Barlow–Proschan importance for component
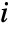 is the probability that the failure of component
is the probability that the failure of component 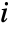 coincides with the failure of the system.
coincides with the failure of the system. - The Barlow–Proschan importance for component
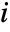 is given by the expectation of Birnbaum importance for component
is given by the expectation of Birnbaum importance for component 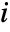 using the
using the 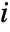
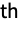 component lifetime distribution.
component lifetime distribution. - The results are returned in the component order given in the distribution list in rdist or fdist.
Examples
open all close allBasic Examples (3)
Two components connected in series, with different lifetime distributions:
The result is given in the same order as the distribution list in ReliabilityDistribution:
Two components connected in parallel, with different lifetime distributions:
Scope (16)
ReliabilityDistribution Models (8)
Two components connected in parallel, with identical lifetime distributions:
Two components connected in series, with identical lifetime distributions:
A system where two out of three components need to work, with identical lifetime distributions:
A simple mixed system with identical lifetime distributions:
A system with a series connection in parallel with a component:
The component ![]() is critical to the system, and therefore most important:
is critical to the system, and therefore most important:
Study the effect of a change in parameter in a simple mixed system:
Show the changes in importance when worsening one of the parallel components:
Any valid ReliabilityDistribution can be used:
The less reliable component ![]() has a much higher risk of coinciding with the failure of the system:
has a much higher risk of coinciding with the failure of the system:
Model the system in steps to get the importance measure for a subsystem:
The subsystem is more reliable, and therefore has a lower risk of coinciding with system failure:
FailureDistribution Models (8)
Any of two basic events lead to the top event:
Only both basic events together lead to the top event:
A voting gate, with identical distributions on the basic events:
A simple system with both And and Or gates:
A simple system with both And and Or gates:
Study the effect of a change in parameter in a simple mixed system:
Show the changes in importance when worsening one of the basic events:
Any valid FailureDistribution can be used:
The standby component is more important:
Model the system in steps to get the importance measure for a subsystem:
Applications (2)
Analyze what component is most likely to have caused a failure at the launch of an aircraft. The hangar door can be opened electronically or manually:
Two fuel pumps require power to run:
Two more pumps run on reliable batteries, giving the following fuel transfer structure:
Also needed is de-icing of the aircraft and a fuel storage tank:
Define the lifetime distributions:
It is very likely that failure of a pump coincides with a failure to launch the aircraft:
Consider a water pumping system, with one valve and two redundant pumps. The reliability of the components are given as probabilities:
It is very likely that failure of the valve coincides with system failure:
Properties & Relations (3)
BarlowProschanImportance is defined as an Expectation of BirnbaumImportance:
BarlowProschanImportance always sums to 1:
Related Guides
History
Text
Wolfram Research (2012), BarlowProschanImportance, Wolfram Language function, https://reference.wolfram.com/language/ref/BarlowProschanImportance.html.
CMS
Wolfram Language. 2012. "BarlowProschanImportance." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/BarlowProschanImportance.html.
APA
Wolfram Language. (2012). BarlowProschanImportance. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BarlowProschanImportance.html
BibTeX
@misc{reference.wolfram_2025_barlowproschanimportance, author="Wolfram Research", title="{BarlowProschanImportance}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/BarlowProschanImportance.html}", note=[Accessed: 15-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_barlowproschanimportance, organization={Wolfram Research}, title={BarlowProschanImportance}, year={2012}, url={https://reference.wolfram.com/language/ref/BarlowProschanImportance.html}, note=[Accessed: 15-January-2026]}