FailureDistribution[bexpr,{{x1,dist1},{x2,dist2},…}]
represents the failure distribution for a system with events xi having reliability distribution disti where the top event occurs when the Boolean expression bexpr is True and event xi has occurred when xi is True.


FailureDistribution
FailureDistribution[bexpr,{{x1,dist1},{x2,dist2},…}]
represents the failure distribution for a system with events xi having reliability distribution disti where the top event occurs when the Boolean expression bexpr is True and event xi has occurred when xi is True.
Details

- FailureDistribution[bexpr,…] corresponds to a fault tree specification.
- The Boolean expression bexpr is also known as the structure function for the system.
- Typical structure functions include:
-
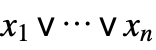
Or gate 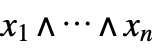
And gate ![TemplateBox[{BooleanCountingFunction, paclet:ref/BooleanCountingFunction}, RefLink, BaseStyle -> {2ColumnTableMod}][{k,n},n] TemplateBox[{BooleanCountingFunction, paclet:ref/BooleanCountingFunction}, RefLink, BaseStyle -> {2ColumnTableMod}][{k,n},n]](Files/FailureDistribution.en/3.png)
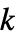 -out-of-
-out-of-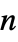 system
systemBooleanConsecutiveFunction[k,n] consecutive- 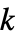 -out-of-
-out-of-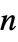 system
system - The structure function bexpr can be any positive unate Boolean function.
- UnateQ[bexpr] can be used to test whether a Boolean expression is positive unate.
- The event reliability distributions disti need to be univariate with PDF[disti,t] zero for t≤0.
- For FailureDistribution[bexpr,…] with event indicators xi:
-
xiTrue indicates event xi has occurred xiFalse indicates event xi has not occurred - The CDF at time t for FailureDistribution[bexpr,{{x1,dist1},…}] is given by Probability[bexpr/.{x1->t1≤t,…},{t1dist1,…}].
- FailureDistribution can be used with such functions as Mean, SurvivalFunction, HazardFunction, and RandomVariate.
Examples
open all close allBasic Examples (3)
Scope (22)
Basic Uses (5)
Find the mean time to failure for a system that fails if either of the two events occur:
Find the survival function for a system that fails if both events occur:
Find the SurvivalFunction of a system that fails when two out of three events occur:
Generate random numbers for a system with different event distributions:
Compare the histogram to the PDF:
Model a system with a component that has standby functionality:
Structure Functions (4)
A system with three events and a voting gate:
A system that fails if at least three out of four events occur:
Any positive unate Boolean expression can used as a structure function:
Use UnateQ to test whether a Boolean expression is positive unate:
Parametric Lifetime Distributions (4)
Use any parametric lifetime distribution including LogNormalDistribution:
Numerically compute the mean time to failure:
Compute the mean time to failure as a function of distribution parameters:
When one event occurs substantially later, it determines the system lifetime:
Define two distributions with the same mean time to failure:
Define systems with Or and And gates with these distributions:
Show how the different mean time to failures vary with ![]() :
:
Discrete lifetime distributions can be used:
Calculate the mean time to failure:
Plot the SurvivalFunction:
Nonparametric Lifetime Distributions (3)
Model airplane glass strength using SmoothKernelDistribution:
Consider a system that fails if either the airplane glass breaks or the other event occurs:
Model events with HistogramDistribution:
Plot the survival function for an Or gate with two and three events:
Model an event directly from data with EmpiricalDistribution:
Plot the survival function when either of two events causes the system to fail:
Derived Lifetime Distributions (6)
Model events with StandbyDistribution:
Calculate the mean time to failure:
Plot SurvivalFunction:
Complex systems can be modeled in steps:
Find the mean time to failure:
This is equivalent to modeling the whole system at once:
Model an event with StandbyDistribution:
The first of two events to occur causes the top event to occur:
Plot the survival function and compare it with only the standby event:
A system where one event is ParameterMixtureDistribution:
Model a two-component cold standby system with MixtureDistribution:
Use it in FailureDistribution and compute the survival function:
Show equivalence with StandbyDistribution:
OrderDistribution can be used to model lifetimes of events:
Plot SurvivalFunction:
Applications (6)
Model the risk of not being woken up in the morning. Assume that an old alarm clock is kept as a backup:
The main alarm clock is electrical:
Define the distributions; the rates are failures per year:
Find the probability of not being woken up at some point during the first year:
Mean time to failure in years:
A problem at coal mines is bulldozers falling through bridged voids in coal piles. The bulldozer can be over a void intentionally or unintentionally:
To form a void, there has to be subsurface flow in the coal. This requires removal of coal from below on a conveyor belt, and an open feeder to that belt:
It is also required that no flow occurs on the surface. This can happen if the coal freezes:
Compacted coal can also lead to a non-flowing surface:
Assume the following distributions for the events:
The probability of the main event happening during a year on one coal pile:
For the 337 piles in the United States:
The mean time to the event happening on one pile is roughly 60 years:
An underwater dry maintenance cabin is used to repair pipelines underwater. The mean time to failure in hours for the life support system components and their life distributions ![]() are given below:
are given below:
First model the air supply subsystem:
Finally, model the air detection system:
The life support system fails if any of the subsystems fail:
The typical mission time is 24 hours. Compute the probability of survival for a mission:
The mean time to failure is considerably larger than the mission time:
Consider a propulsion system that provides thrust to a vehicle in orbit around the Earth. We model the event of applying thrust after the device has been turned off:
Failure of the timing relay to open:
The structure for failure of relief valve 1 to close:
The structure for failure of relief valve 2 to close:
The unwanted propulsion occurs if both relief valves fail to close:
Compute the mean time to an unwanted propulsion:
Find the probability of unwanted propulsion occurring during a mission that lasts six months:
A system has the following structure and lifetime distribution:
Find the requirement on the failure rate ![]() to avoid failure during a mission of five days with a probability of
to avoid failure during a mission of five days with a probability of ![]() :
:
FailureDistribution can be used as a generalized OrderDistribution:
This is equal to OrderDistribution if identical distributions are used:
Properties & Relations (12)
FailureDistribution uses local names for variables in the input:
Hence, subsequent computations can be done with the original variable name:
The probability that neither of two failure events occur before ![]() :
:
This corresponds to an Or gate:
The probability that both failure events did not occur before ![]() :
:
This corresponds to an And gate:
The probability that no two failure events occur before ![]() :
:
This corresponds to a two-out-of-three voting gate:
An Or gate connecting identical events corresponds to an OrderDistribution:
An And gate connecting identical events corresponds to an OrderDistribution:
A voting gate with identical events corresponds to an OrderDistribution:
The lifetime of Or gate-connected basic events is the minimum of the component lifetimes:
The lifetime of two events connected with an And gate is the maximum of the event lifetimes:
A ![]() -out-of-
-out-of-![]() voting gate corresponds to TransformedDistribution with a RankedMin function:
voting gate corresponds to TransformedDistribution with a RankedMin function:
Compare the survival functions:
Exponentially distributed events connected by an Or gate give an exponential top event:
Weibull distributed events connected by an Or gate give a Weibull distributed top event:
FailureDistribution models that if the failure of ![]() or
or ![]() occurs, the top event occurs:
occurs, the top event occurs:
ReliabilityDistribution models that both components have to work for the system to work:
Components ![]() and
and ![]() working is equivalent to the event of either
working is equivalent to the event of either ![]() or
or ![]() failing:
failing:
Model that two out of four components need to fail for the system to fail:
This is equal to that three out of four components need to work for the system to work:
Possible Issues (3)
Component distributions need to have a positive domain:
Use TruncatedDistribution to restrict the domain to positive values only:
Exact or symbolic properties cannot always be computed:
Approximate values can typically still be found:
A FailureDistribution is only well defined for positive unate structure expressions:
Use UnateQ to test whether a Boolean expression is positive unate:
History
Text
Wolfram Research (2012), FailureDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/FailureDistribution.html.
CMS
Wolfram Language. 2012. "FailureDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FailureDistribution.html.
APA
Wolfram Language. (2012). FailureDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FailureDistribution.html
BibTeX
@misc{reference.wolfram_2025_failuredistribution, author="Wolfram Research", title="{FailureDistribution}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/FailureDistribution.html}", note=[Accessed: 24-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_failuredistribution, organization={Wolfram Research}, title={FailureDistribution}, year={2012}, url={https://reference.wolfram.com/language/ref/FailureDistribution.html}, note=[Accessed: 24-January-2026]}