StandbyDistribution

StandbyDistribution[dist1,{dist2,…,distn}]

represents a standby distribution with component lifetime distributions disti. When component i fails, component i+1 will become active.

StandbyDistribution[dist1,{dist2,…,distn},p]

represents a standby distribution where switching from component i to component i+1 succeeds with probability p.

StandbyDistribution[dist1,{dist2,…,distn},sdist]

represents a standby distribution where the switch component has lifetime distribution sdist.

StandbyDistribution[dist1,{…,{disti,inactive,disti,active},…},…]

represents a standby distribution where the i^(th) component lifetime distribution follows disti,inactive in inactive mode and disti,active in active mode.

Details

  • StandbyDistribution[…,…] represents a system with perfect switching where transitioning between components always succeeds.
  • StandbyDistribution[…,…,s] represents a system with imperfect switching. If s is a distribution, it represents that lifetime of the switch; otherwise it represents the probability of a successful transition between components.
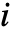
  • StandbyDistribution[…,{…,Ai,…},…] represents a standby distribution where the 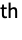i^(th) component follows a cold standby distribution Ai when it is active, and does not deteriorate when it is inactive.
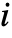
  • StandbyDistribution[…,{…,{Ii,Ai},…},…] represents a standby distribution where the 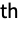i^(th) component follows a warm standby distribution. The component deteriorates following distribution Ii when it is inactive and distribution Ai when it is active.
  • Any mix of cold and warm standby component distributions can be used.
  • The survival function and other properties for StandbyDistribution can be derived from the equivalent TransformedDistribution[expr,dists] with the distribution assumptions dists given by {a1A1,a2A2,…,i2I2,i3I3,…,sS,uUniformDistribution[{0,1}]}.
  • StandbyDistribution[…]TransformedDistribution[…,dists]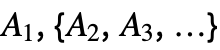
    A_(1),{A_(2),A_(3),...}a1+a2+a3+⋯
    A1,{A2,A3,…},pa1+ a2Boole[p>u]+a3Boole[p2>u]+⋯
    A1,{A2,A3,…},Sa1+a2Boole[s>a1]+a3Boole[s>a1+a2]+⋯
    A1,{{I2,A2},{I3,A3},…}a1+a2Boole[i2>a1]+a3Boole[i3>a1+a2Boole[i2>a1]]+⋯
    A1,{{I2,A2},{I3,A3},…},pa1+a2 Boole[i2>a1∧p>u]+a3Boole[i3>a1+ a2Boole[i2>a1]∧p2>u]+⋯
    A1,{{I2,A2},{I3,A3},…},Sa1+a2 Boole[i2>a1∧s>a1]+a3Boole[i3>a1+a2Boole[i2>a1]∧s>a1+a2Boole[i2>a1]]+⋯
  • StandbyDistribution can be used with such functions as Mean, SurvivalFunction, HazardFunction, ReliabilityDistribution, and RandomVariate.

Examples

open allclose all

Basic Examples  (3)

Define a cold standby system with perfect switching:

Compute its PDF:

Mean time to failure:

Compare to a non-standby system:

Define a cold standby system with imperfect switching:

Compute its PDF:

Mean time to failure:

Compare to a non-standby system:

Define cold and warm standby systems, with inactive failure rate half the active failure rate:

Compute the mean time to failure:

Compare the survival functions:

Scope  (17)

Cold Standby and Perfect Switching  (3)

Define a cold standby system with three identical components:

Compute mean time to failure:

Define a cold standby system with two different components:

Compute the survival function:

Study a component with three identical components in standby:

Generate random variates:

Compare with the probability density function:

Cold Standby and Imperfect Switching  (4)

A cold standby system where the switch succeeds with probability p:

Find the mean time to failure:

Compare perfect switching to imperfect switching where the switch works half the time:

A cold standby system where the switch is modeled by a lifetime distribution:

Find the survival function:

Study the effect of having worse switches:

Cold standby system with three components and a switch modeled by a distribution:

Generate random variates:

Compare with the probability density function:

A switch modeled with a probability of success:

Compare with the probability density:

Warm Standby and Perfect Switching  (3)

Standby system where the component can fail while in standby:

Find the mean time to failure:

System with multiple components that can fail in standby:

Compare the survival function to a cold standby system:

Warm standby system with two components in standby:

Generate random variates:

Compare with the probability density function:

Warm Standby and Imperfect Switching  (4)

Warm standby system where the switch succeeds with a probability p:

Compute the mean time to failure:

Warm standby system where the switch has a lifetime distribution:

Compute the mean time to failure:

Warm standby system where the switch is modeled with a lifetime distribution:

Generate random variates:

Compare with the probability density function:

System where the switch succeeds with a probability:

Mixed Warm and Cold Standby Systems  (3)

Standby system where the second component can fail while in standby:

The system where the second and third component switch places:

Compare the survival functions:

A mixed cold and warm standby system, where the switch succeeds with probability 0.9`:

Find the hazard function:

Generate random numbers and compare with probability density:

Standby system where one component can fail while in standby, and a switch with a lifetime:

Compare the survival functions with different switch failure rates:

Applications  (2)

The lifetime of a component is exponentially distributed. To improve reliability, a second identical component is acquired. Find the most efficient use of this second component:

One alternative is a parallel configuration:

Another alternative is a standby configuration, with a switch that succeeds with probability p:

Plot the survival function of the two alternatives and compare with the original component, assuming perfect switching:

Simulate failure times for 30 standby systems and find the best configuration:

Check how bad a switch you can use while still being better than a parallel system:

The requirement on the switch to equal a parallel system gets lower with time:

Consider a computer server. It requires a power supply, hard drives, a network card, and a router to fulfill its intended function. The power supply is backed by a backup power outlet and a diesel generator in cold standby:

The hard drives are in a RAID configuration, which requires 2 out of 3 to work:

The network card has a second card in standby:

Two routers are connected in parallel:

The resulting survival function:

Plot it:

Compute the mean time to failure numerically:

Find the probability that the server survives for three months:

Define a consumer version that does not contain any redundancy:

Compare the survival functions:

Properties & Relations  (9)

Cold standby corresponds to the sum of component lifetimes:

Compare the survival functions:

Cold standby with identical exponentially distributed components is an ErlangDistribution:

Cold standby where component lifetimes follow the ExponentialDistribution corresponds to the HypoexponentialDistribution:

StandbyDistribution is a special case of TransformedDistribution:

Compare the survival functions:

StandbyDistribution is a special case of MixtureDistribution:

Compare the probability density function:

StandbyDistribution can be used in ReliabilityDistribution:

Compute the survival function:

ReliabilityDistribution can be used in StandbyDistribution:

Generate random numbers:

Compare with the probability density function:

StandbyDistribution can be used in FailureDistribution:

Compute the survival function:

FailureDistribution can be used in StandbyDistribution:

Generate random numbers:

Compare with the probability density function:

Possible Issues  (1)

Component distributions need to have a positive domain:

Use TruncatedDistribution to restrict the domain to positive values only:

Wolfram Research (2012), StandbyDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/StandbyDistribution.html.

Text

Wolfram Research (2012), StandbyDistribution, Wolfram Language function, https://reference.wolfram.com/language/ref/StandbyDistribution.html.

CMS

Wolfram Language. 2012. "StandbyDistribution." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/StandbyDistribution.html.

APA

Wolfram Language. (2012). StandbyDistribution. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/StandbyDistribution.html

BibTeX

@misc{reference.wolfram_2024_standbydistribution, author="Wolfram Research", title="{StandbyDistribution}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/StandbyDistribution.html}", note=[Accessed: 21-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_standbydistribution, organization={Wolfram Research}, title={StandbyDistribution}, year={2012}, url={https://reference.wolfram.com/language/ref/StandbyDistribution.html}, note=[Accessed: 21-December-2024 ]}