CylindricalDecompositionFunction
CylindricalDecompositionFunction[data][x1,x2,…]
x1,x2,…における円柱代数式を表す.
詳細とオプション

- CylindricalDecompositionFunction[…][x1,x2,…]はCylindricalDecomposition[expr, {x1,x2,…},"Function"]によって生成される.
- CylindricalDecompositionFunctionオブジェクトは半代数的集合の明示的にコンパクトな表現を与える.これを使ってさらに効率的な計算を行うことができる.
- CylindricalDecompositionFunctionは,集合の論理結合の計算,追加的な条件による集合の制限,変数の除去,集合の最適化を含む,半代数的集合の反復的計算によく使われる.
- x1,…,xn における円柱代数式は
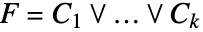 の形をしている.ただし,
の形をしている.ただし,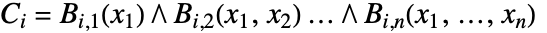 である.各
である.各 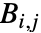 の形は
の形は 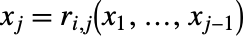 または
または 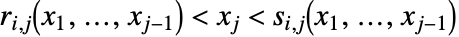 である.
である.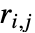 と
と 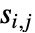 は
は 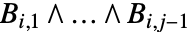 の解集合で定義される連続的な代数関数である.
の解集合で定義される連続的な代数関数である.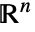 における
における 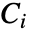 の解集合
の解集合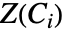 はセルと呼ばれる.任意の
はセルと呼ばれる.任意の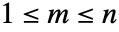 についてのセル
についてのセル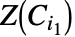 と
と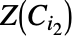 の
の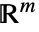 上への写像は,互いに素であるか同一であるかのどちらかである.
上への写像は,互いに素であるか同一であるかのどちらかである. - CylindricalDecompositionFunctionは円柱代数式のカプセル化された表現を与える.この表現は,CylindricalDecompositionFunctionやCylindricalDecomposition,あるいはReduce,Resolve,FindInstance,Solve,Minimize等のソルバへの入力の中で使われる際にしばしばより効率的である.
- NormalはCylindricalDecompositionFunctionオブジェクトを等式と不等式の明示的な論理結合に変換する.
例題
すべて開くすべて閉じる例 (2)
スコープ (23)
基本的な用法 (7)
一定の真理値を持つCylindricalDecompositionFunctionを簡約するとTrueまたはFalseになる:
最初の引数が実数であるCylindricalDecompositionFunctionは自動的に簡約される:
CylindricalDecompositionFunctionオブジェクトを以降の計算に使う:
代数的マッピングを使ってCylindricalDecompositionFunctionを合成する:
CylindricalDecompositionFunctionオブジェクトと多項式不等式の論理結合を使う:
ブール演算 (2)
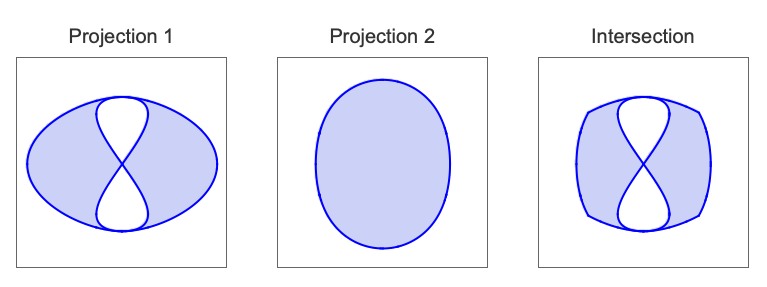
定量化された系のCylindricalDecompositionFunction解 ![]() を計算する:
を計算する:
異なる2つの定量化された系のCylindricalDecompositionFunction解を計算する:
等式と不等式を解く (2)
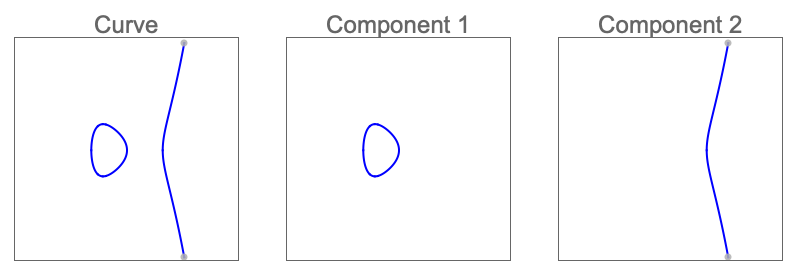
定量化された系のCylindricalDecompositionFunction解 ![]() を計算する:
を計算する:
CylindricalDecompositionFunctionオブジェクト,方程式,不等式の論理結合を解く:
限定子の消去 (3)
定量化されたCylindricalDecompositionFunctionオブジェクトから限定子を消去する:
変数が式に現れるのと同じ順序で定量化されている場合に限定子を消去する:
CylindricalDecompositionFunctionオブジェクトを含む系から限定子を消去する:
定量化された変数が自由変数の後で式に現れる場合は,消去は速い:
位相操作 (5)
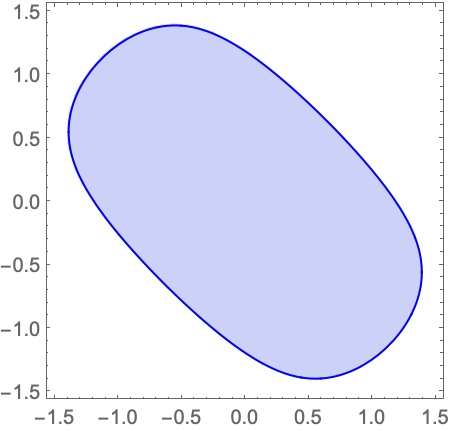
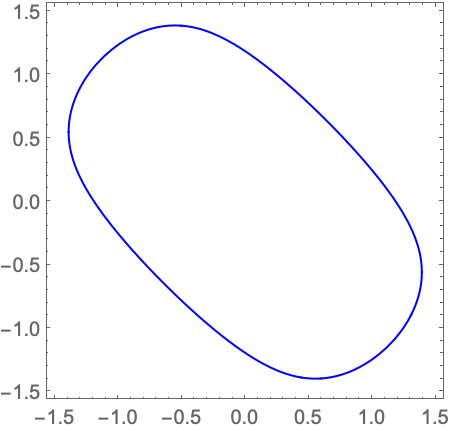
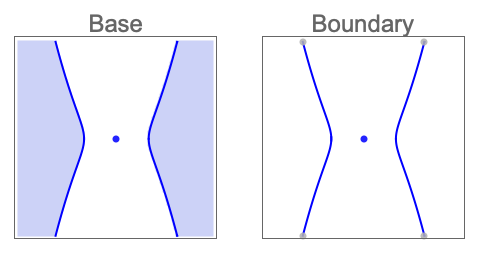
解の領域とその境界のCylindricalDecompositionFunction表現を求める:
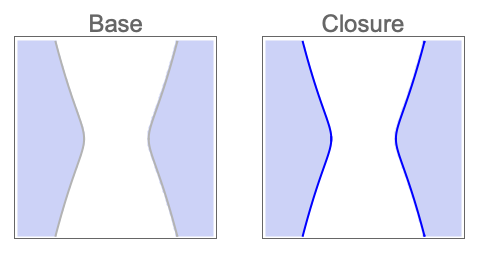
解の領域とその閉包のCylindricalDecompositionFunction表現を求める:
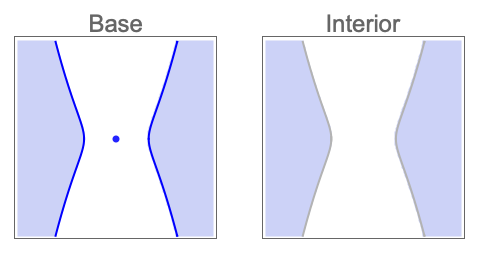
解の領域とその内部のCylindricalDecompositionFunction表現を求める:
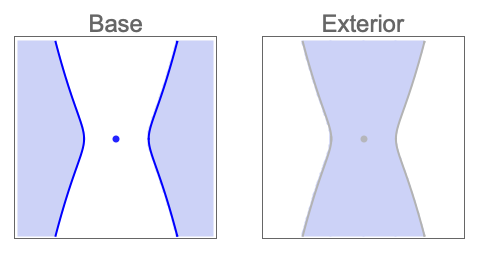
解の領域とその外部のCylindricalDecompositionFunction表現を求める:
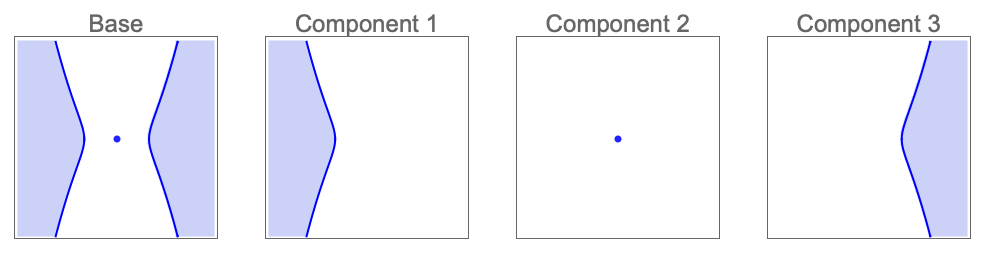
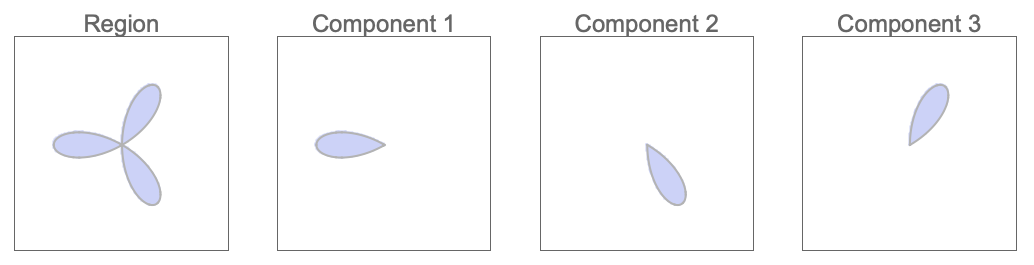
解の領域とその連結成分のCylindricalDecompositionFunction表現を求める:
ソルバへの入力としてのCylindricalDecompositionFunction (4)
CylindricalDecompositionFunctionを使って最適化制約を指定する:
方程式,不等式,CylindricalDecompositionFunctionの制約を含む系を解く:
FindInstanceを使ってCylindricalDecompositionFunctionを含む系についての解の例を求める:
CylindricalDecompositionFunctionの解集合の各連結成分に含まれる点を少なくとも1つずつ求める:
特性と関係 (5)
デフォルトで,CylindricalDecompositionは明示的な等式と不等式として書かれた式を与える:
CylindricalDecompositionFunctionのNormalは等しく,しばしば直接計算された式と同一である:
カプセル化形式の円柱代数式は続く計算でより効率的なことが多い:
CylindricalDecompositionFunctionオブジェクトに対する操作は速い:
明示的な等式と不等式として書かれた円柱楕円式に対する操作は,はるかに遅くなることが多い:
FindInstanceを使ってCylindricalDecompositionFunctionオブジェクトを満たす点を求める:
SemialgebraicComponentInstancesは,半代数集合の各連結成分で少なくとも1つの点を与える:
CylindricalDecompositionFunctionは複数のセルをまとめてよりコンパクトな表現にする:
SemialgebraicComponentInstancesは,より少ない点で十分なことが分かった:
GenericCylindricalDecompositionは半代数集合の表現を低次元の部分まで計算する:
Method{"CylindricalDecompositionFunctionOutput"True}を使ってCylindricalDecompositionFunctionの結果を得る:
考えられる問題 (1)
CylindricalDecompositionFunctionは,非厳密な引数を与えられると,比較のために引数の非厳密な値を使うが,厳密な結果を生成する:
テキスト
Wolfram Research (2020), CylindricalDecompositionFunction, Wolfram言語関数, https://reference.wolfram.com/language/ref/CylindricalDecompositionFunction.html.
CMS
Wolfram Language. 2020. "CylindricalDecompositionFunction." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CylindricalDecompositionFunction.html.
APA
Wolfram Language. (2020). CylindricalDecompositionFunction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CylindricalDecompositionFunction.html