DStabilityConditions

DStabilityConditions[eqn,x[t],t]

微分方程式の固定点と安定条件を与える．

DStabilityConditions[{eqn1,eqn2,…},{x1[t],x2[t],…},t]

微分方程式系の固定点と安定条件を与える．

DStabilityConditions[{eqn1,eqn2,…},{x1[t],x2[t],…},t,{pnt1,pnt2,…}]

指定された固定点についてのみ安定条件を与える．

詳細とオプション

  • 安定性は近似安定性として，固定点は平衡点または停留点としても知られている．
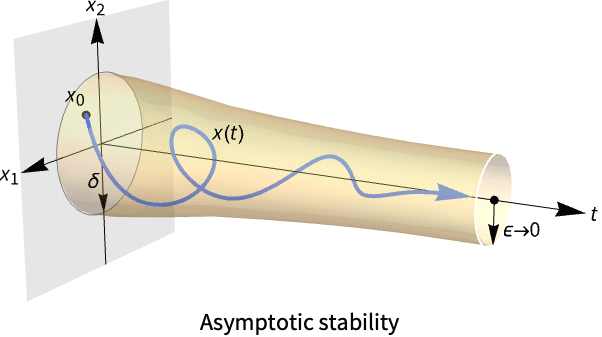
  • DStabilityConditionsは，固定点近くの長期的な挙動の定性的解析によく使われる．系が安定しているなら，十分近ければ解は固定点に収束する．
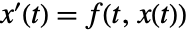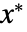  • 微分方程式の系 の点 は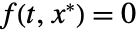，のときかつそのときに限って固定点である．事実，初期値 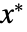は固定点のままで， で初期化したなら 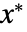に留まる．
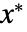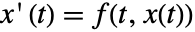  • 固定点 は，で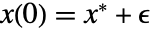 のときに限り，漸近的に安定している．十分小さい 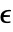についてTemplateBox[{{x, (, t, )}, t, infty}, Limit2Arg]=x^*である．
  • DStabilityConditionsは{{{,,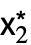…},cond},…} の形のリストを返す．ただし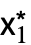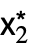，{,,…}は固定点である．
  • DStabilityConditionsは固定点の局所的な安定性に十分な条件を与える．線形系については，これらの条件は大域的安定性の条件でもある．
  • DStabilityConditionsは線形および非線形の常微分方程式に使うことができる．
  • 次は，使用できるオプションである．
  • Assumptions $Assumptionsパラメータについての仮定

例題

すべて開くすべて閉じる

例  (7)

方程式 の固定点を求め，その安定性を判定する：

方程式 の固定点を求め，その安定性を判定する：

方程式 の固定点と安定性の条件を求める：

a のさまざまな値についていくつかの解をプロットする：

二次元の系についての安定性解析：

系が安定するパラメータ領域をプロットする：

非線形微分方程式の安定性解析：

StreamPlotを使って安定性を示す：

定数係数を持つ線形系の安定性：

StreamPlotを使って安定性を可視化する：

非線形方程式の固定点を求める：

最初の点の安定性を調べる：

2番目の点の安定性を調べる：

スコープ  (21)

線形方程式  (5)

方程式 の固定点を求め，その安定性を判定する：

一次線形非同次方程式：

のときの不安定解をプロットする：

のときの安定解をプロットする：

二次線形方程式：

パラメータ と について，安定領域をプロットする：

三次線形方程式：

安定領域をプロットする：

より高次の非同次常微分方程式：

固定点の座標を初期値として使って常微分方程式を解く：

非線形方程式  (2)

一次非線形方程式の安定性：

初期値 についての解をプロットする：

StreamPlotを使って における安定性を示す：

二次非線形常微分方程式について考える：

DSolveは，この方程式を解くことができない：

DStabilityConditionsを使ってこの方程式の安定性を解析する：

この方程式を一次常微分方程式の系に変換する：

平面におけるこの系の軌跡をプロットする：

線形系  (10)

非連立方程式の安定した線形系：

系の軌跡：

非連立方程式の不安定な線形系：

系の軌跡：

定数係数を持つ不安定な系：

定数係数を持つ安定した系：

虚数の固有値を持つ一次の系：

StreamPlotを使って安定性を可視化する：

非同次の不安定な系：

非同次の安定した系：

解をプロットする：

記号係数を持つ線形系：

Assumptionsを使って安定性条件を簡約する：

4つの線形常微分方程式の系：

解をプロットする：

ランダムな定数係数を持つ10×10線形系の安定性を解析する：

非線形系  (4)

非線形の一次の系：

StreamPlotを使って安定性を可視化する：

周期的な固定点を持つ非線形系：

原点に不安定な固定点を持つ非線形系：

3つの常微分方程式の非線形系：

結果を簡約する：

オプション  (2)

Assumptions  (2)

Assumptionsがないと，安定性についてのパラメータの条件が付く：

Assumptionsを使うと，条件が簡約されることが多い：

2つの非線形方程式の系は無数の周期的固定点を持つ：

Assumptionsを使って従属変数の範囲を指定する：

アプリケーション  (11)

物理学  (5)

減衰をともなうバネ・質量系の安定性解析を行う：

仮定を使って安定性条件を簡約する：

バネ・質量系の方程式を解く：

パラメータの与えられた値について解をプロットする：

電気回路の方程式の安定性解析を行う：

電気回路の方程式を解く：

パラメータの与えられた値について解をプロットする：

減衰した振子方程式の安定性解析：

系の相図をプロットする：

初期条件 ，についての解をプロットする：

Lorenz方程式の安定した系：

StreamPlot3D を使ってLorenzアトラクタを可視化する：

Lorenz方程式の不安定な系：

系を解いて解をプロットする：

生物学  (3)

捕食者被食者モデル（Lotka–Volterra方程式）の安定性解析：

系の相図をプロットする：

初期条件 ，について系を解く：

解をプロットする：

Rosenzweig–MacArthurの捕食者被食者モデル：

ケモスタットモデルは，微生物が非生物資源で成長する生物学的系を表す：

，についての系の安定性を解析する：

化学  (1)

ブラッセレータは，一種の自己触媒反応の理論モデルである．

ブラッセレータモデルのレート方程式：

系の固定点を求める：

b<1+a2ならこの点は安定している：

b>1+a2なら，この点は不安定である：

制御系  (2)

オイラーの運動方程式から始めて衛星の姿勢力学を解析する：

主慣性モーメント, , のオイラーの方程式：

, , の固定値について方程式の安定性を解析する：

固定点を作用点として選択する：

状態空間モデルを構築する：

衛星の姿勢は，妨害されると調整できない：

モデルの可制御性を検証する：

ラグランジュ(Lagrangian)を使って倒立振子について調べる：

の位置：

速度：

台車と振子の運動エネルギー：

振子の位置エネルギー：

ラグランジュ：

一般化された力：

運動方程式：

状態空間モデル：

非正の固有値で系は不安定になる：

特性と関係  (9)

DStabilityConditionsは，微分方程式の固定点と安定性条件を返す：

DFixedPointsを使って微分方程式のすべての固定点を求める：

特定の固定点における安定性を解析する：

DFixedPointsを使って非線形常微分方程式のすべての固定点を求める：

Solveを使って固定点を求める：

最初の固定点近くで方程式を線形化する：

最初の固定点近くでの安定性をチェックする：

2番目の固定点近くで方程式を線形化する：

2番目の固定点近くの安定性をチェックする：

DStabilityConditionsを使って非線形方程式の安定性を判定する：

n 次微分方程式の固定点は， n 次元ベクトルである：

n 個の一次微分方程式の系の固定点は，n 次元ベクトルである：

2つの常微分方程式の系の安定性を解析する：

固定点を初期条件として使って，DSolveValueで系を解く：

与えられた初期条件についてDSolveValueを使って系を解く：

解をプロットする：

非線形常微分方程式の安定性を解析する：

NDSolveを使って常微分方程式を解く：

解をプロットする：

非線形常微分方程式の安定性を解析する：

最初の固定点を初期条件として使って常微分方程式の漸近解を計算する：

別の初期条件についての常微分方程式の漸近解を計算する：

2つの非線形常微分方程式の系の固定点を求める：

系のヤコビ行列を計算する：

各固定点についてヤコビ行列の固有値を計算する：

すべての固有値が負の実部を持つなら，この系は固定点近くで局所的に安定している：

DStabilityConditionsを使って点の安定性をチェックする：

考えられる問題  (2)

場合によっては，安定性の条件が最も単純ではないことがある：

さらに処理することでもっと簡約することができる：

与えられた点が混合整数ではないので，DStabilityConditionsはうまくいかない：

まず，DFixedPoints を使って方程式のすべての固定点を求める：

おもしろい例題  (2)

van der Pol振動子は，非保存的な，非線形減衰がある振動する系である：

系の安定性を解析する：

パラメータ のさまざまな値について，系の軌道をアニメーション化する：

FitzHugh–Nagumoモデルは弛緩振動子の例である：

外部からの刺激 s が特定の閾値を超えると，系は変数 x および y が弛緩して静止値に戻る前に位相空間における特徴的な偏位を示す：

パラメータ s のさまざまな値について系の軌跡を可視化する：

Wolfram Research (2024), DStabilityConditions, Wolfram言語関数， https://reference.wolfram.com/language/ref/DStabilityConditions.html.

テキスト

Wolfram Research (2024), DStabilityConditions, Wolfram言語関数， https://reference.wolfram.com/language/ref/DStabilityConditions.html.

CMS

Wolfram Language. 2024. "DStabilityConditions." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DStabilityConditions.html.

APA

Wolfram Language. (2024). DStabilityConditions. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DStabilityConditions.html

BibTeX

@misc{reference.wolfram_2024_dstabilityconditions, author="Wolfram Research", title="{DStabilityConditions}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/DStabilityConditions.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_dstabilityconditions, organization={Wolfram Research}, title={DStabilityConditions}, year={2024}, url={https://reference.wolfram.com/language/ref/DStabilityConditions.html}, note=[Accessed: 21-November-2024 ]}