DStabilityConditions

DStabilityConditions[eqn,x[t],t]

gives the fixed points and stability conditions for a differential equation.

DStabilityConditions[{eqn1,eqn2,…},{x1[t],x2[t],…},t]

gives the fixed points and stability conditions for a system of differential equations.

DStabilityConditions[{eqn1,eqn2,…},{x1[t],x2[t],…},t,{pnt1,pnt2,…}]

gives the stability conditions for the given fixed points.

Details and Options

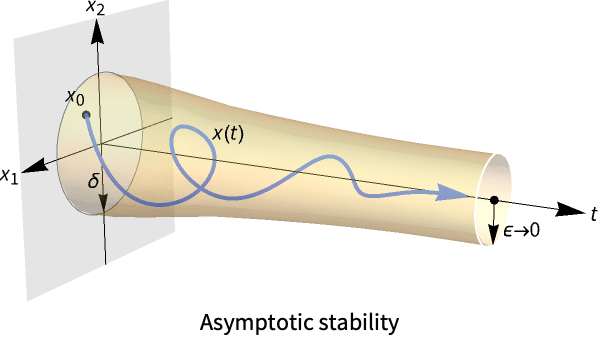
  • Stability is also known as asymptotic stability, and fixed points are also known as equilibrium points or stationary points.
  • DStabilityConditions is typically used to qualitatively analyze long-term behavior near fixed points. If the system is stable, then solutions converge to the fixed point if you are close enough.
  • For a system of differential equations 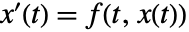, a point 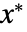is a fixed point iff 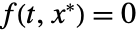. In effect, the initial value 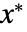remains stationary; if you initialize at 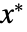you stay at .
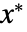  • A fixed point 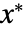is asymptotically stable iff for 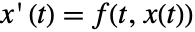and 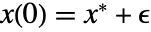you have TemplateBox[{{x, (, t, )}, t, infty}, Limit2Arg]=x^* for 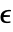sufficiently small.
  • DStabilityConditions returns a list of the form {{{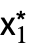,,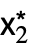…},cond},…}, where {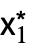,,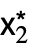…} is a fixed point.
  • DStabilityConditions gives sufficient conditions for local stability of fixed points. For linear systems, these conditions are also conditions for global stability.
  • DStabilityConditions works for linear and nonlinear ordinary differential equations.
  • The following options can be given:
  • Assumptions $Assumptionsassumptions on parameters

Examples

open allclose all

Basic Examples  (7)

Find the fixed point and determine its stability for the equation :

Find the fixed point and determine the stability for the equation :

Find the fixed points and conditions for stability for the equation :

Plot several solutions for different values of a:

Stability analysis of a two-dimensional system:

Plot the parameter region for which the system is stable:

Stability analysis of a nonlinear differential equation:

Use StreamPlot to demonstrate the stability:

The stability of a linear system with constant coefficients:

Use StreamPlot to visualize the stability:

Find the fixed points for a nonlinear equation:

Study the stability of the first point:

Study the stability of the second point:

Scope  (21)

Linear Equations  (5)

Find the fixed point and determine its stability for the equation :

A first-order linear inhomogeneous equation:

Plot the unstable solution for :

Plot the stable solution for :

Second-order linear equation:

Plot the stability region for parameters and :

Third-order linear equation:

Plot the stability region:

Higher-order inhomogeneous ODE:

Solve the ODE using coordinates of the fixed point as initial values:

Nonlinear Equations  (2)

The stability of a first-order nonlinear equation:

Plot the solution for the initial value :

Use StreamPlot to demonstrate the stability at :

Consider a second-order nonlinear ODE:

DSolve is unable to solve this equation:

Analyze the stability of the equation using DStabilityConditions:

Transform the equation into a system of first-order ODEs:

Plot the trajectories of the system in the plane:

Linear Systems  (10)

A stable linear system of uncoupled equations:

Trajectories of the system:

An unstable linear system of uncoupled equations:

Trajectories of the system:

Unstable system with constant coefficients:

Stable system with constant coefficients:

A first-order system with imaginary eigenvalues:

Use StreamPlot to visualize the stability:

Inhomogeneous unstable system:

Inhomogeneous stable system:

Plot the solutions:

Linear system with symbolic coefficients:

Use Assumptions to simplify the stability conditions:

System of four linear ODEs:

Plot the solutions:

Analyze the stability of a 10×10 linear system with random constant coefficients:

Nonlinear Systems  (4)

A nonlinear first-order system:

Use StreamPlot to visualize the stability:

A nonlinear system with periodic fixed points:

A nonlinear system with unstable fixed point at origin:

A nonlinear system of three ODEs:

Simplify the result:

Options  (2)

Assumptions  (2)

Without Assumptions, there are conditions on parameters for stability:

Using Assumptions can often result in simplified conditions:

A system of two nonlinear equations has an infinite number of periodic fixed points:

Use Assumptions to specify the range of a dependent variable:

Applications  (11)

Physics  (5)

Do stability analysis for the spring-mass system with damping:

Use assumptions to simplify the stability conditions:

Solve the spring-mass system equation:

Plot the solution for given values of parameters:

Do stability analysis for the electric circuit equation:

Solve the electric circuit equation:

Plot the solution for given values of parameters:

Stability analysis for the damped pendulum equation:

Plot the phase portrait of the system:

Plot the solution for the initial conditions , :

Stable system of Lorenz equations:

Use StreamPlot3D to visualize the Lorenz attractors:

Unstable system of Lorenz equations:

Solve the system and plot the solution:

Biology and Ecology  (3)

Stability analysis for the predator-prey model (Lotka–Volterra equation):

Plot the phase portrait of the system:

Solve the system for the initial conditions , :

Plot the solutions:

The Rosenzweig–MacArthur predator-prey model:

The chemostat model represents biological systems in which microorganisms grow on abiotic resources:

Analyze the stability of the model for and :

Chemistry  (1)

The Brusselator is a theoretical model for a type of autocatalytic reaction.

The rate equations of the Brusselator model:

Find the fixed point of the system:

The point is stable if b<1+a2:

The point is unstable if b>1+a2:

Control Systems  (2)

Analyze a satellite's attitude dynamics starting from Euler's equations of motion:

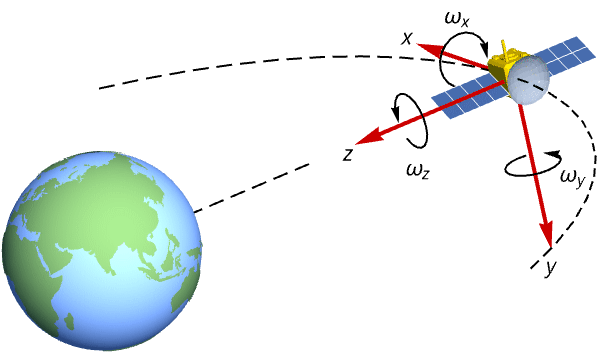
Euler’s equations with principal moments of inertia , , :

Analyze the stability of the equation for fixed values of , , :

Choose the fixed point as an operating point:

Construct a state-space model:

The satellite’s attitude is unregulated if disturbed:

Verify the controllability of the model:

Study an inverted pendulum using the Lagrangian:

The position of :

Its velocity:

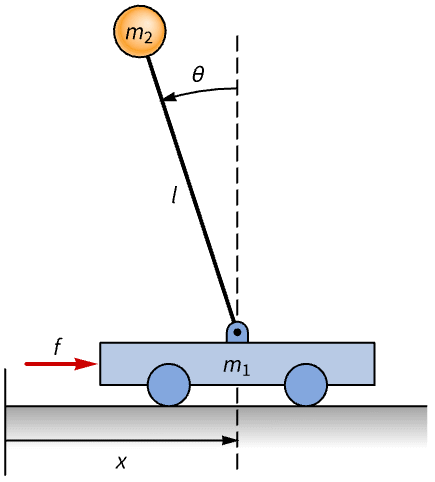
The kinetic energy of the cart and pendulum:

The potential energy of the pendulum:

The Lagrangian:

The generalized forces:

The equations of motion:

A state-space model:

The non-positive eigenvalues make it an unstable system:

Properties & Relations  (9)

DStabilityConditions returns fixed points and stability conditions for differential equations:

Use DFixedPoints to find all fixed points of a differential equation:

Analyze the stability at specific fixed points:

Use DFixedPoints to find all fixed points of a nonlinear ODE:

Use Solve to find the fixed points:

Linearize the equation near the first fixed point:

Check the stability near the first fixed point:

Linearize the equation near the second fixed point:

Check the stability near the second fixed point:

Determine the stability of a nonlinear equation using DStabilityConditions:

The fixed points for the n^(th)-order differential equation are n-dimensional vectors:

The fixed points for the system of n first-order differential equations are n-dimensional vectors:

Analyze the stability of a system of two ODEs:

Use DSolveValue to solve the system using a fixed point as initial condition:

Use DSolveValue to solve the system for given initial conditions:

Plot the solution:

Analyze the stability of a nonlinear ODE:

Solve the ODE using NDSolve:

Plot the solution:

Analyze the stability of a nonlinear ODE:

Calculate an asymptotic solution of the ODE using the first fixed point as initial condition:

Calculate an asymptotic solution of the ODE for another initial condition:

Find the fixed points for the system of two nonlinear ODEs:

Calculate the Jacobian matrix of the system:

Calculate the eigenvalues of the Jacobian matrix for each fixed point:

The system is locally stable near the fixed point if all of the eigenvalues have negative real parts:

Check the stability of the points using DStabilityConditions:

Possible Issues  (2)

Sometimes the conditions for stability are not the simplest possible:

Additional simplification can be achieved by further processing:

DStabilityConditions fails because the given point is not a fixed point:

Use DFixedPoints to find all fixed points of the equation first:

Neat Examples  (2)

The van der Pol oscillator is a non-conservative, oscillating system with nonlinear damping:

Analyze the stability of the system:

Animate the trajectories of the system for various values of the parameter :

The FitzHugh–Nagumo model is an example of a relaxation oscillator:

If the external stimulus s exceeds a certain threshold value, the system will exhibit a characteristic excursion in phase space, before the variables x and y relax back to their rest values.

Visualize the trajectories of the system for various values of the parameter s:

Wolfram Research (2024), DStabilityConditions, Wolfram Language function, https://reference.wolfram.com/language/ref/DStabilityConditions.html.

Text

Wolfram Research (2024), DStabilityConditions, Wolfram Language function, https://reference.wolfram.com/language/ref/DStabilityConditions.html.

CMS

Wolfram Language. 2024. "DStabilityConditions." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DStabilityConditions.html.

APA

Wolfram Language. (2024). DStabilityConditions. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DStabilityConditions.html

BibTeX

@misc{reference.wolfram_2024_dstabilityconditions, author="Wolfram Research", title="{DStabilityConditions}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/DStabilityConditions.html}", note=[Accessed: 07-September-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_dstabilityconditions, organization={Wolfram Research}, title={DStabilityConditions}, year={2024}, url={https://reference.wolfram.com/language/ref/DStabilityConditions.html}, note=[Accessed: 07-September-2024 ]}