DirichletCharacter
DirichletCharacter[k,j,n]
法が k,インデックスが j のディリクレ(Dirichlet)指標 ![]() を与える.
を与える.
詳細

- 記号操作・数値操作の両方に適した数学的整数関数である.
- DirichletCharacter[k, j, n]は k を法とした可能なディリクレ指標の特定の順序を選ぶ.
- 与えられた法 k に対し,インデックス j でラベルが付けられた ϕ
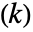 個の異なるディリクレ指標が存在する.変換方法が異なると可能な指標の順序も異なることがある.
個の異なるディリクレ指標が存在する.変換方法が異なると可能な指標の順序も異なることがある. - DirichletCharacter[k,j,n]は n 中で周期 k で周期的である.
- DirichletCharacter[k,j,n]は n が k と互いに素ではない場合はゼロである.
- DirichletCharacter[k,j,n]は n において乗法関数である.
例題
すべて開くすべて閉じるスコープ (3)
アプリケーション (5)
DirichletCharacterから一般化されたベルヌーイ(Bernoulli)数を定義する:
一般化されたベルヌーイ数を使ってDirichletLの負の整数における値を計算する:
単位指標の0における一般化されたベルヌーイ数は![]() でそれ以外は0である:
でそれ以外は0である:
![]() と
と ![]() を法として
を法として ![]() と互いに素である値におけるその指標の積はガウスの総和を与える:
と互いに素である値におけるその指標の積はガウスの総和を与える:
![]() を法とした原始指標について,
を法とした原始指標について,![]() は
は ![]() と互いに素ではない値では0である:
と互いに素ではない値では0である:
![]() を法とした原始指標について,ガウスの総和の絶対値は
を法とした原始指標について,ガウスの総和の絶対値は![]() に等しい:
に等しい:
DirichletCharacter[25,11,n]の導手は5である:
特性と関係 (11)
DirichletCharacterは周期的である:
DirichletCharacterは完全に乗法的である:
![]() を法としたDirichletCharacterは
を法としたDirichletCharacterは ![]() と互いに素である値においては非零である:
と互いに素である値においては非零である:
![]() を法としたDirichletCharacterは
を法としたDirichletCharacterは ![]() と互いに素ではない値においては零である:
と互いに素ではない値においては零である:
![]() を法とした原始指標のインデックスは
を法とした原始指標のインデックスは![]() で
で ![]() と互いに素である値については
と互いに素である値については![]() を,その他については
を,その他については![]() を与える:
を与える:
JacobiSymbol[n,k]は奇整数 k について k を法とした実数のディリクレ指標である:
k を法とした実数の原始指標 χ はJacobiSymbol[χ[-1]k,n]と定義できる:
実数の原始的ではない指標は ![]() と互いに素である整数においてはJacobiSymbolを使って書くことができる:
と互いに素である整数においてはJacobiSymbolを使って書くことができる:
DirichletCharacter[k,j,n]は k の原始根 n が存在する場合はそこで![]() を与える:
を与える:
DirichletCharacterの乗法特性を使って ![]() と互いに素である整数における値を求める:
と互いに素である整数における値を求める:
![]() を法とした指標は
を法とした指標は ![]() の素数ベキを法とした記号の積として書くことができる:
の素数ベキを法とした記号の積として書くことができる:
32 5と互いに素であるすべての整数について分解式を検証する:
テキスト
Wolfram Research (2008), DirichletCharacter, Wolfram言語関数, https://reference.wolfram.com/language/ref/DirichletCharacter.html.
CMS
Wolfram Language. 2008. "DirichletCharacter." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DirichletCharacter.html.
APA
Wolfram Language. (2008). DirichletCharacter. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DirichletCharacter.html