DiscreteHadamardTransform
DiscreteHadamardTransform[list]
给出 list 的离散阿达马变换.
更多信息和选项

- DiscreteHadamardTransform 也称作沃尔什转换和沃尔什-阿达马转换.
- 默认情况下,长度为
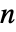 的列表
的列表 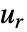 的离散阿达马变换
的离散阿达马变换 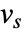 定义为
定义为 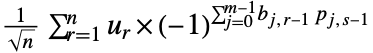 ,其中
,其中 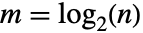 ,
,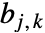 是整数
是整数 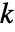 的二进制表示法中的第
的二进制表示法中的第 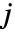
 比特位,而
比特位,而 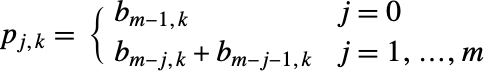 .
. - DiscreteHadamardTransform 返回一个长度为2的幂的列表. 如果输入 list 的长度不是 2 的幂,那么使用零对其填充直至达到一个大于
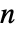 的2的最小的幂.
的2的最小的幂. - DiscreteHadamardTransform 包含一个 Method 选项,用于指定变换的序列排序(阿达马基序列中的过零次数). 可能的设置包括:
-
"BitComplement" 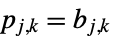
"GrayCode" "BitComplement" 的格雷(Gray)码重新排序 "Sequency" 顺序随行和列索引的增加而增加(默认) - 比特补码排序也称为西尔维斯特(Sylvester)排序.
- 序列排序也称为沃尔什(Walsh)排序.
- 格雷(Gray)码排序也称为二元排序或帕利(Paley)排序.
- 正、 逆阿达马变换是相同的. »
范例
打开所有单元关闭所有单元属性和关系 (3)
离散阿达马变换是其自身的逆(对合函数,involution):
DiscreteHadamardTransform 自动使用零填充到2的最接近的幂:
带有格雷码排序的阿达马变换等价于将格雷码排列应用于带有比特补码序列排序的阿达马变换:
Wolfram Research (2012),DiscreteHadamardTransform,Wolfram 语言函数,https://reference.wolfram.com/language/ref/DiscreteHadamardTransform.html (更新于 2024 年).
文本
Wolfram Research (2012),DiscreteHadamardTransform,Wolfram 语言函数,https://reference.wolfram.com/language/ref/DiscreteHadamardTransform.html (更新于 2024 年).
CMS
Wolfram 语言. 2012. "DiscreteHadamardTransform." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2024. https://reference.wolfram.com/language/ref/DiscreteHadamardTransform.html.
APA
Wolfram 语言. (2012). DiscreteHadamardTransform. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/DiscreteHadamardTransform.html 年