FourierDST

FourierDST[list]

finds the Fourier discrete sine transform of a list of real numbers.

FourierDST[list,m]

finds the Fourier discrete sine transform of type .

Details

  • Possible types 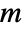of discrete sine transform for a list 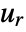of length 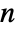giving a result 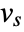are:
  • 1 (DST-I)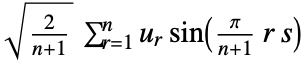
    2 (DST-II)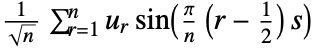
    3 (DST-III)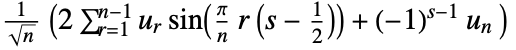
    4 (DST-IV)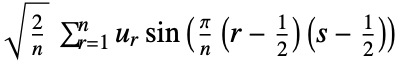
  • FourierDST[list] is equivalent to FourierDST[list,2].
  • The inverse discrete sine transforms for types 1, 2, 3, 4 are types 1, 3, 2, 4, respectively.
  • The list given in FourierDST[list] can be nested to represent an array of data in any number of dimensions.
  • The array of data must be rectangular.
  • If the elements of list are exact numbers, FourierDST begins by applying N to them.
  • FourierDST can be used on SparseArray objects.

Examples

open allclose all

Basic Examples  (2)

Find a discrete sine transform:

Find the inverse discrete sine transform:

Find a discrete sine transform of type 1 (DST-I):

Find the inverse discrete sine transform:

Scope  (2)

Use machine arithmetic to compute the discrete sine transform:

Use 24‐digit precision arithmetic:

Two-dimensional discrete sine transform:

Four-dimensional discrete sine transform:

Generalizations & Extensions  (2)

The list may have complex values:

You can use "I", "II", "III", or "IV" for the types 1, 2, 3, and 4 respectively:

Applications  (2)

Sine Series Expansion  (1)

Get an expansion for an odd function as a sum of sines:

The function values on a uniformly spaced grid with n points on [-L,L):

Compute the DST-I and renormalize:

The function has, in effect, been periodized with a particular odd symmetry:

Plot the expansion error where the points are defined:

Pseudospectral PDE Discretization  (1)

Approximate the second derivative for a function with zero boundary conditions:

Solve the wave equation for a plucked string:

Plot the solution as a surface:

Properties & Relations  (3)

DST-I and DST-IV are their own inverses:

DST-II and DST-III are inverses of each other:

The DST is equivalent to matrix multiplication:

Possible Issues  (1)

FourierDST always returns normalized results:

To get unnormalized results, you can multiply by the normalization:

Wolfram Research (2007), FourierDST, Wolfram Language function, https://reference.wolfram.com/language/ref/FourierDST.html.

Text

Wolfram Research (2007), FourierDST, Wolfram Language function, https://reference.wolfram.com/language/ref/FourierDST.html.

CMS

Wolfram Language. 2007. "FourierDST." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FourierDST.html.

APA

Wolfram Language. (2007). FourierDST. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FourierDST.html

BibTeX

@misc{reference.wolfram_2024_fourierdst, author="Wolfram Research", title="{FourierDST}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/FourierDST.html}", note=[Accessed: 18-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_fourierdst, organization={Wolfram Research}, title={FourierDST}, year={2007}, url={https://reference.wolfram.com/language/ref/FourierDST.html}, note=[Accessed: 18-December-2024 ]}