DiscreteMaxLimit
DiscreteMaxLimit[f,k∞]
gives the max limit k∞f(k) of the sequence f as k tends to ∞ over the integers.
DiscreteMaxLimit[f,{k1![]() ,…,kn
,…,kn![]() }]
}]
gives the nested max limit ![]() ⋯
⋯ ![]() f(k1,…,kn) over the integers.
f(k1,…,kn) over the integers.
DiscreteMaxLimit[f,{k1,…,kn}{![]() ,…,
,…,![]() }]
}]
gives the multivariate max limit ![]() f(k1,…,kn) over the integers.
f(k1,…,kn) over the integers.
Details and Options



- DiscreteMaxLimit is also known as limit superior, supremum limit, limsup, upper limit and outer limit.
- DiscreteMaxLimit computes the smallest upper bound for the limit and is always defined for real-valued sequences. It is often used to give conditions of convergence and other asymptotic properties that do not rely on an actual limit to exist.
- DiscreteMaxLimit[f,k∞] can be entered as
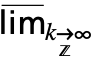 f. A template
f. A template 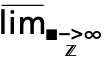 can be entered as
can be entered as  dMlim
dMlim , and
, and  moves the cursor from the underscript to the body.
moves the cursor from the underscript to the body. - DiscreteMaxLimit[f,{k1,…,kn}{
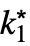 ,…,
,…,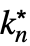 }] can be entered as
}] can be entered as 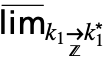 …
…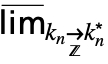 f.
f. - The possible limit points
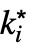 are ±∞.
are ±∞. - The max limit is defined as a limit of the max envelope sequence max[ω]:
-
DiscreteMaxLimit[f,k∞] DiscreteLimit[max[ω],ω∞] DiscreteMaxLimit[f,{k1,…,kn}{∞,…,∞}] DiscreteLimit[max[ω],ω∞] - DiscreteMaxLimit[f[k],k-∞] is equivalent to DiscreteMaxLimit[f[-l],l∞] etc.
- The definition uses the max envelope max[ω]MaxValue[{f[k],k≥ω∧k∈
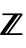 },k] for univariate f[k] and max[ω]MaxValue[{f[k1,…,kn],k1≥ω∧⋯∧kn≥ω∧ki∈
},k] for univariate f[k] and max[ω]MaxValue[{f[k1,…,kn],k1≥ω∧⋯∧kn≥ω∧ki∈ },{k1,…,kn}] for multivariate f[k1,…,kn]. The sequence max[ω] is monotone decreasing as ω∞, so it always has a limit, which may be ±∞.
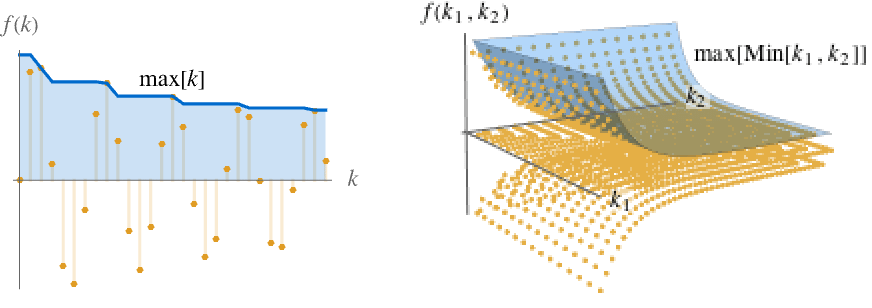
},{k1,…,kn}] for multivariate f[k1,…,kn]. The sequence max[ω] is monotone decreasing as ω∞, so it always has a limit, which may be ±∞. - The illustration shows max[k] and max[Min[k1,k2]] in blue.
- DiscreteMaxLimit returns unevaluated when the max limit cannot be found.
- The following options can be given:
-
Assumptions $Assumptions assumptions on parameters GenerateConditions Automatic whether to generate conditions on parameters Method Automatic method to use PerformanceGoal "Quality" aspects of performance to optimize - Possible settings for GenerateConditions include:
-
Automatic non-generic conditions only True all conditions False no conditions None return unevaluated if conditions are needed - Possible settings for PerformanceGoal include $PerformanceGoal, "Quality" and "Speed". With the "Quality" setting, DiscreteMaxLimit typically solves more problems or produces simpler results, but it potentially uses more time and memory.
Examples
open allclose allBasic Examples (4)
Use ![]() dMlim
dMlim![]() to enter the template
to enter the template ![]() and
and ![]() to move from the underscript to the body:
to move from the underscript to the body:
TraditionalForm typesetting:
Scope (21)
Basic Uses (4)
Elementary Sequences (6)
Periodic Sequences (3)
Piecewise Sequences (2)
Special Function Sequences (2)
Options (6)
Assumptions (1)
GenerateConditions (3)
Return a result without stating conditions:
This result is only valid if x>1:
Return unevaluated if the results depend on the value of parameters:
By default, conditions are generated that return a unique result:
By default, conditions are not generated if only special values invalidate the result:
With GenerateConditions->True, even these non-generic conditions are reported:
Method (1)
PerformanceGoal (1)
DiscreteMaxLimit computes limits involving sequences of arbitrarily large periods:
Use PerformanceGoal to avoid potentially expensive computations in such cases:
The Method option overrides PerformanceGoal:
Applications (7)
Basic Applications (2)
Compute the asymptotic supremum of a sequence:
Plot the sequence and the asymptotic supremum:
Verify that the following sequence does not have a limit:
Show that DiscreteMaxLimit and DiscreteMinLimit are not equal:
Confirm that the limit does not exist by using DiscreteLimit:
Series Convergence (4)
Show that the infinite series whose general term is defined here is convergent, by using the ratio test:
Plot the partial sums of the series:
Compute the ratio of the adjacent terms using DiscreteRatio:
The sequence of ratios does not converge:
However, the ratio test can still be used because the upper limit of the ratios is less than 1:
Confirm that the series converges using SumConvergence:
Show that the infinite series whose general term is defined here is convergent, by using the root test:
Plot the partial sums of the series:
Compute the n![]() root of the general term:
root of the general term:
The limit of the sequence of roots does not exist:
However, the root test still indicates convergence because the max limit is less than 1:
Confirm that the series converges using SumConvergence:
The inverse radius of the associated power series ![]() is given by:
is given by:
This means the radius of convergence is infinite and converges for all ![]() , in particular to
, in particular to ![]() :
:
Compute the Taylor series at zero and its radius of convergence for the following function:
Formally, the Taylor series does sum to the original function:
The radius of convergence of the Taylor series is given by:
This means the Taylor series will converge for values of ![]() within
within ![]() of the origin. For example, at
of the origin. For example, at ![]() :
:
At values of ![]() further away, the sum will not converge; for example, at
further away, the sum will not converge; for example, at ![]() :
:
At the points ![]() , the terms of the Taylor series alternate between
, the terms of the Taylor series alternate between ![]() and
and ![]() :
:
Hence the partial sums go between ![]() and
and ![]() :
:
Visualize ![]() and the partial sums of its Taylor series on the interval
and the partial sums of its Taylor series on the interval ![]() ; in the interior of the interval, convergence is rapid, but the Taylor polynomials always go to either
; in the interior of the interval, convergence is rapid, but the Taylor polynomials always go to either ![]() or
or ![]() at the endpoints:
at the endpoints:
Computational Complexity (1)
An algorithm runtime function ![]() is said to be "big-o of
is said to be "big-o of ![]() ", written
", written ![]() , if
, if ![]() :
:
Similarly, ![]() is said to be "big-theta of
is said to be "big-theta of ![]() ", written
", written ![]() if
if ![]() and
and ![]() :
:
It is possible for two functions to share neither relationship:
Hence, ![]() defines a reflexive partial order on the space of algorithm runtimes similar to
defines a reflexive partial order on the space of algorithm runtimes similar to ![]() :
:
If ![]() and
and ![]() , then
, then ![]() , which implies that
, which implies that ![]() is an equivalence relation:
is an equivalence relation:
Properties & Relations (11)
A real-valued sequence always has a (possibly infinite) max limit:
The corresponding limit may not exist:
If ![]() and
and ![]() have finite max limits, then
have finite max limits, then ![]() :
:
In this case, there is strict inequality:
Positive multiplicative constants can be moved outside a limit:
For a real-valued sequence, if DiscreteLimit exists, DiscreteMaxLimit has the same value:
DiscreteMaxLimit is always greater than or equal to DiscreteMinLimit:
If DiscreteMaxLimit equals DiscreteMinLimit, the limit exists and equals their common value:
If the max limit is ![]() , then the min limit and thus the limit are also
, then the min limit and thus the limit are also ![]() :
:
DiscreteMaxLimit can be computed as -DiscreteMinLimit[-f,…]:
If the two max limits are equal—as in this example—then ![]() has a limit:
has a limit:
This is a generalization of the "squeezing" or "sandwich" theorem:
MaxLimit is always greater than or equal to DiscreteMaxLimit:
Possible Issues (1)
DiscreteMaxLimit is only defined for real-valued sequences:
Text
Wolfram Research (2017), DiscreteMaxLimit, Wolfram Language function, https://reference.wolfram.com/language/ref/DiscreteMaxLimit.html.
CMS
Wolfram Language. 2017. "DiscreteMaxLimit." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DiscreteMaxLimit.html.
APA
Wolfram Language. (2017). DiscreteMaxLimit. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiscreteMaxLimit.html