Prime[n]
gives the n![]() prime number
prime number ![]() .
.


Prime
Prime[n]
gives the n![]() prime number
prime number ![]() .
.
Details
- Prime is also known as prime number sequence.
- Integer mathematical function, suitable for both symbolic and numerical manipulation.
![TemplateBox[{n}, Prime] TemplateBox[{n}, Prime]](Files/Prime.en/3.png) is the smallest positive integer greater than
is the smallest positive integer greater than ![TemplateBox[{{n, -, 1}}, Prime] TemplateBox[{{n, -, 1}}, Prime]](Files/Prime.en/4.png) , which cannot be divided by any integer greater than 1 and smaller than itself. The first prime
, which cannot be divided by any integer greater than 1 and smaller than itself. The first prime ![TemplateBox[{1}, Prime] TemplateBox[{1}, Prime]](Files/Prime.en/5.png) is the integer 2.
is the integer 2.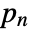 is asymptotically equivalent to
is asymptotically equivalent to 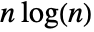 as
as 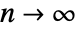 .
.
Examples
open all close allBasic Examples (3)
Scope (10)
Numerical Evaluation (4)
Applications (38)
Basic Applications (9)
Visualize the primes with a parabolic sieve:
Visualize the sieve of Eratosthenes for the first 5 primes:
Find the lowest-divisor pair for an integer ![]() :
:
Find the factorization for an integer ![]() :
:
Construct a factorization tree for an integer ![]() :
:
Visualize prime numbers with periodic curves. Prime numbers are those where only two curves cross—its own and the curve of 1:
Approximations (3)
Number Theory (14)
Plot of the first 50 primes modulo 6:
Fraction of the first million primes greater than 3 of the form ![]() :
:
With the exception of 2 and 3, all primes are of the form ![]() :
:
Define a residue number system:
Choose two numbers and represent them in the residue system:
Multiplying and recovering in the residue system:
An approximation to the zeta function:
Calculate the probability that a number is relatively prime to the first 25 primes:
Differences between the first 100 primes:
Find the jumping champion, i.e. the most frequently occurring difference between consecutive primes:
Calculate the sum of prime factors:
Plot the sum of prime factors for the first 25 integers:
Find Goldbach partitions, i.e. pairs of primes (![]() ,
, ![]() ) such that
) such that ![]() :
:
Graph Goldbach's conjecture/comet:
Calculate the primorial up to the nthprime, i.e. a function that multiplies successive primes, similar to the factorial:
Compare the primorial to the factorial up to ![]() :
:
Plot the differences between the factorial and the primorial up to ![]() :
:
Plot the Chebyshev theta function:
Calculate the prime powers up to ![]() :
:
Count all the prime powers up to ![]() :
:
Graph the sequence of prime powers:
It is conjectured that for any integer ![]() , there is a prime
, there is a prime ![]() with
with ![]() :
:
Verify this for a range of integers:
Plot Andrica's conjecture, which states that √pn+1-√pn<1 for every pair of consecutive prime numbers pn and pn+1:
Plot Brocard's conjecture, which states that if pn and pn+1 are consecutive primes greater than 2, then between (pn)2 and (pn+1)2 there are at least four prime numbers:
Plot polynomials for ![]() -gons, i.e. Chebyshev polynomials of the second kind, such that
-gons, i.e. Chebyshev polynomials of the second kind, such that ![]() is prime:
is prime:
Special Sequences (12)
Find twin primes, i.e. pairs of primes of the form ![]() :
:
A prime ![]() is a Sophie Germain prime if
is a Sophie Germain prime if ![]() is also a prime:
is also a prime:
There are 5 Fermat primes, i.e. Fermat numbers ![]() such that
such that ![]() is prime:
is prime:
There are two Wieferich primes under ![]() , i.e. a prime number
, i.e. a prime number ![]() such that
such that ![]() divides
divides ![]() :
:
Construct prime Euclid numbers:
Pythagorean primes can be written as the sum of two squares, i.e. a prime number ![]() :
:
Ramanujan primes are the smallest number Rn such that π(x) - π(x/2) ≥ n for all x≥ Rn:
Differences in nth Ramanujan primes and Prime:
Primes of the form ![]() , i.e. prime elements of the Gaussian integers:
, i.e. prime elements of the Gaussian integers:
Array plot of the Gaussian primes, a Gaussian integer ![]() such that if
such that if ![]() and
and ![]() are nonzero, then
are nonzero, then ![]() is prime or if
is prime or if ![]() ,
, ![]() or if
or if ![]() ,
, ![]() :
:
Emirp primes are primes ![]() whose reversal is also prime but not a palindrome:
whose reversal is also prime but not a palindrome:
Find home primes of ![]() .
. ![]() is found by concatenating the prime factors of
is found by concatenating the prime factors of ![]() and repeating until a prime is reached:
and repeating until a prime is reached:
Properties & Relations (8)
The traditional mathematical notation for Prime:
Primes represents the domain of all prime numbers:
The largest domain of definitions of Prime:
Prime is asymptotically equivalent to ![]() as
as ![]() :
:
PrimePi is the inverse of Prime:
Use NextPrime to find the next prime above n:
PrimeOmega counts the number of prime divisors:
EulerPhi[n] counts numbers less than or equal to ![]() that are coprime to
that are coprime to ![]() :
:
Neat Examples (6)
Ulam spiral colored based on the difference in Prime values:
Visualize when ![]() is divisible by primes. Each row of dots corresponds to the divisors of
is divisible by primes. Each row of dots corresponds to the divisors of ![]() , which are labelled along the horizontal axis:
, which are labelled along the horizontal axis:
Generate a path based on the Prime sequence:
Construct polyhedra using directed graphs generated by primes less than ![]() :
:
See Also
NextPrime RandomPrime PrimeQ PrimePowerQ CompositeQ PrimePi Primes PrimeZetaP Zeta MersennePrimeExponent FactorInteger PerfectNumber EulerPhi
Function Repository: LargestPrimeGap TwinPrimes TwinPrime
History
Introduced in 1988 (1.0) | Updated in 2020 (12.1)
Text
Wolfram Research (1988), Prime, Wolfram Language function, https://reference.wolfram.com/language/ref/Prime.html (updated 2020).
CMS
Wolfram Language. 1988. "Prime." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2020. https://reference.wolfram.com/language/ref/Prime.html.
APA
Wolfram Language. (1988). Prime. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Prime.html
BibTeX
@misc{reference.wolfram_2025_prime, author="Wolfram Research", title="{Prime}", year="2020", howpublished="\url{https://reference.wolfram.com/language/ref/Prime.html}", note=[Accessed: 08-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_prime, organization={Wolfram Research}, title={Prime}, year={2020}, url={https://reference.wolfram.com/language/ref/Prime.html}, note=[Accessed: 08-March-2026]}