PrimeOmega

PrimeOmega[n]

gives the number of prime factors counting multiplicities in n.

Details and Options

  • Integer mathematical function, suitable for both symbolic and numerical manipulation.
  • PrimeOmega gives the number of prime factors of an integer with multiplicity.
  • For a number 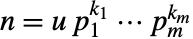with a unit and primes, PrimeOmega[n] returns k1+⋯+km.
  • With the setting GaussianIntegers->True, PrimeOmega gives the number of Gaussian prime factors.
  • PrimeOmega[m+In] automatically works over Gaussian integers.

Examples

open allclose all

Basic Examples  (2)

Compute PrimeOmega at 30:

Plot the PrimeOmega sequence for the first 100 numbers:

Scope  (8)

Numerical Evaluation  (4)

PrimeOmega works over integers:

Gaussian integers:

Compute for large integers:

PrimeOmega threads over lists:

Symbolic Manipulation  (4)

TraditionalForm formatting:

Reduce expressions:

Solve equations:

Identify the PrimeOmega sequence:

Options  (1)

GaussianIntegers  (1)

Compute PrimeOmega over integers:

Gaussian integers:

Applications  (6)

Basic Applications  (2)

Table of the values of PrimeOmega for the integers up to 100:

Histogram of the values of PrimeOmega:

Number Theory  (4)

Use PrimeOmega to test for a prime number:

Use PrimeOmega to compute LiouvilleLambda:

Compare with:

Plot the average over values of PrimeOmega for different ranges of integer arguments:

The Fourier statistics of the PrimeOmega sequence:

Properties & Relations  (5)

Use FactorInteger to find the number of prime factors counting multiplicities:

PrimeOmega is a completely additive function:

PrimeOmega gives the exponent for a prime power:

PrimeOmega and PrimeNu are equivalent when the argument is square-free:

PrimeOmega is always greater than or equal to PrimeNu:

Possible Issues  (1)

PrimeOmega is not defined at 0:

Neat Examples  (2)

Plot the arguments of the Fourier transform of PrimeOmega:

Plot the Ulam Spiral of PrimeOmega:

Wolfram Research (2008), PrimeOmega, Wolfram Language function, https://reference.wolfram.com/language/ref/PrimeOmega.html.

Text

Wolfram Research (2008), PrimeOmega, Wolfram Language function, https://reference.wolfram.com/language/ref/PrimeOmega.html.

CMS

Wolfram Language. 2008. "PrimeOmega." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PrimeOmega.html.

APA

Wolfram Language. (2008). PrimeOmega. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PrimeOmega.html

BibTeX

@misc{reference.wolfram_2025_primeomega, author="Wolfram Research", title="{PrimeOmega}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/PrimeOmega.html}", note=[Accessed: 23-May-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_primeomega, organization={Wolfram Research}, title={PrimeOmega}, year={2008}, url={https://reference.wolfram.com/language/ref/PrimeOmega.html}, note=[Accessed: 23-May-2025 ]}