PrimeNu

PrimeNu[n]

gives the number of distinct primes in n.

Details and Options

  • Integer mathematical function, suitable for both symbolic and numerical manipulation.
  • PrimeNu gives the number of distinct prime factors.
  • For a number 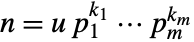with 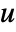a unit and 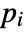primes, PrimeNu[n] returns m.
  • With the setting GaussianIntegers->True, PrimeNu gives the number of Gaussian prime factors.
  • PrimeNu[m+In] automatically works over Gaussian integers.

Examples

open allclose all

Basic Examples  (2)

Compute PrimeNu at 24:

Plot the PrimeNu sequence for the first 100 numbers:

Scope  (9)

Numerical Evaluation  (4)

PrimeNu works over integers:

Gaussian integers:

Compute for large integers:

PrimeNu threads over lists:

Symbolic Manipulation  (5)

TraditionalForm formatting:

Reduce expressions:

Solve equalities:

Identify the PrimeNu sequence:

Dirichlet generating function of 2^PrimeNu:

Compare with DirichletTransform:

Options  (1)

GaussianIntegers  (1)

Compute PrimeNu over integers:

Gaussian integers:

Applications  (7)

Basic Applications  (2)

Table of the values of PrimeNu for the integers up to 100:

Histogram of the values of PrimeNu:

Number Theory  (5)

Use PrimeNu to test for a prime power:

Use PrimeNu to compute MoebiusMu and LiouvilleLambda for square-free numbers:

PrimeNu is related to MoebiusMu through the following formula:

Plot the average over values of PrimeNu for different ranges of integer arguments:

The Fourier statistics of the PrimeNu sequence:

Properties & Relations  (6)

Use FactorInteger to find the number of distinct prime factors:

PrimeNu is an additive function:

PrimeNu gives 1 for a prime power:

PrimeNu and PrimeOmega are equivalent when the argument is square free:

PrimeNu is always smaller than or equal to PrimeOmega:

If n is square free, PrimeNu is related to MoebiusMu and LiouvilleLambda:

Possible Issues  (1)

PrimeNu is not defined at 0:

Neat Examples  (2)

Plot the arguments of the Fourier transform of PrimeNu:

Plot the Ulam spiral of PrimeNu:

Wolfram Research (2008), PrimeNu, Wolfram Language function, https://reference.wolfram.com/language/ref/PrimeNu.html.

Text

Wolfram Research (2008), PrimeNu, Wolfram Language function, https://reference.wolfram.com/language/ref/PrimeNu.html.

CMS

Wolfram Language. 2008. "PrimeNu." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PrimeNu.html.

APA

Wolfram Language. (2008). PrimeNu. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PrimeNu.html

BibTeX

@misc{reference.wolfram_2024_primenu, author="Wolfram Research", title="{PrimeNu}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/PrimeNu.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_primenu, organization={Wolfram Research}, title={PrimeNu}, year={2008}, url={https://reference.wolfram.com/language/ref/PrimeNu.html}, note=[Accessed: 21-November-2024 ]}