DiscreteMaxLimit[f,k∞]
k が ∞ に近付くときの数列 f の最大極限k∞f(k) を整数上で与える.
DiscreteMaxLimit[f,{k1![]() ,…,kn
,…,kn![]() }]
}]
ネストした最大極限![]() ⋯
⋯ ![]() f(k1,…,kn)を整数上で与える.
f(k1,…,kn)を整数上で与える.
DiscreteMaxLimit[f,{k1,…,kn}{![]() ,…,
,…,![]() }]
}]
多変量最大極限![]() f(k1,…,kn)を整数上で与える.
f(k1,…,kn)を整数上で与える.




DiscreteMaxLimit
DiscreteMaxLimit[f,k∞]
k が ∞ に近付くときの数列 f の最大極限k∞f(k) を整数上で与える.
DiscreteMaxLimit[f,{k1![]() ,…,kn
,…,kn![]() }]
}]
ネストした最大極限![]() ⋯
⋯ ![]() f(k1,…,kn)を整数上で与える.
f(k1,…,kn)を整数上で与える.
DiscreteMaxLimit[f,{k1,…,kn}{![]() ,…,
,…,![]() }]
}]
多変量最大極限![]() f(k1,…,kn)を整数上で与える.
f(k1,…,kn)を整数上で与える.
詳細とオプション



- DiscreteMaxLimitは,上極限としても知られている.
- DiscreteMaxLimitは極限の最小上界を計算し,常に実数値数列について定義される.収束条件や実際に極限が存在するかどうかに依存しないその他の漸近的特性を与えるためにしばしば使われる.
- DiscreteMaxLimit[f,k∞]は
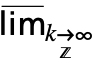 f として入力することができる.テンプレート
f として入力することができる.テンプレート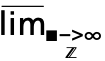 は
は dMlim
dMlim で入力し,
で入力し, を使ってカーソルを真下付き文字から本体に移動する.
を使ってカーソルを真下付き文字から本体に移動する. - DiscreteMaxLimit[f,{k1,…,kn}{
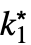 ,…,
,…,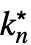 }]は
}]は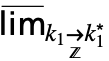 …
…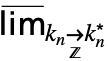 f として入力できる.
f として入力できる. - 可能な極限点
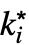 は±∞である.
は±∞である. - 最大極限は最大包絡線数列max[ω]の極限として定義される.
-
DiscreteMaxLimit[f,k∞] DiscreteLimit[max[ω],ω∞] DiscreteMaxLimit[f,{k1,…,kn}{∞,…,∞}] DiscreteLimit[max[ω],ω∞] - DiscreteMaxLimit[f[k],k-∞]はDiscreteMaxLimit[f[-l],l∞]等と等価である.
- この定義は,一変量の f[k]については最大包絡線 max[ω]MaxValue[{f[k],k≥ω∧k∈
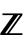 },k]を,多変量の f[k1,…,kn]についてはmax[ω]MaxValue[{f[k1,…,kn],k1≥ω∧⋯∧kn≥ω∧ki∈
},k]を,多変量の f[k1,…,kn]についてはmax[ω]MaxValue[{f[k1,…,kn],k1≥ω∧⋯∧kn≥ω∧ki∈ },{k1,…,kn}]を使う.数列max[ω]は ω∞のとき単調減少であるので,常に極限を持つ.それは±∞である可能性がある.
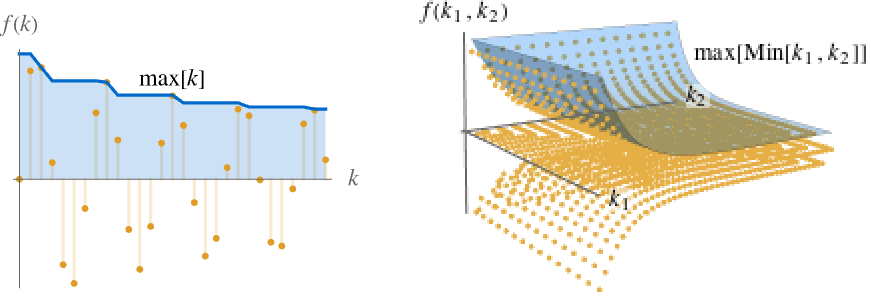
},{k1,…,kn}]を使う.数列max[ω]は ω∞のとき単調減少であるので,常に極限を持つ.それは±∞である可能性がある. - 次の図ではmax[k]とmax[Min[k1,k2]]が青で示されている.
- 最大極限が求まらなかったとき,DiscreteMaxLimitは未評価で返される.
- 次は使用可能なオプションである.
-
Assumptions $Assumptions パラメータについての仮定 GenerateConditions Automatic パラメータについての条件を生成するかどうか Method Automatic 使用するメソッド PerformanceGoal "Quality" パフォーマンスのどの面について最適化するか - 次はGenerateConditionsの可能な設定である.
-
Automatic 一般的ではない条件のみ True すべての条件 False 条件なし None 条件が必要な場合は未評価で返す - PerformanceGoalの可能な設定には,$PerformanceGoal,"Quality","Speed"がある."Quality"設定のとき,DiscreteMaxLimitは,一般に,より多くの問題を解いたりより簡単な結果を与えたりすることが多いが,より多くの時間とメモリが必要になる可能性がある.
例題
すべて開く すべて閉じる例 (4)
スコープ (21)
基本的な用法 (4)
特殊関数数列 (2)
オプション (6)
GenerateConditions (3)
デフォルトで,特別な値だけが結果を無効にするなら条件は生成されない:
GenerateConditions->Trueのときは,一般的ではない条件さえもレポートされる:
PerformanceGoal (1)
DiscreteMaxLimitは,任意に大きい周期の数列を含む極限を計算する:
PerformanceGoalを使って,そのような場合に高くつくかもしれない計算を避ける:
MethodオプションはPerformanceGoalをオーバーライドする:
アプリケーション (7)
基本的な応用 (2)
DiscreteMaxLimitとDiscreteMinLimitは等しくないことを示す:
DiscreteLimitを使って極限が存在しないことを確認する:
級数収束 (4)
以下で一般項が定義されている無限級数が収束することを,比判定法を使って示す:
DiscreteRatioを使って隣接項の比を計算する:
SumConvergenceを使ってこの級数が収束することを確認する:
一般項が以下で定義される無限級数が収束することを,ベキ根判定法を使って示す:
しかし,最大極限が1未満なので,ベキ根判定法は収束を示唆している:
SumConvergenceを使ってこの級数が収束することを確認する:
これは,収束半径が無限ですべての ![]() について,特に
について,特に![]() に収束することを意味している:
に収束することを意味している:
次の関数について,0におけるテイラー(Taylor)級数とその収束半径を計算する:
これは,テイラー級数が原点から![]() 以内で
以内で ![]() の値について収束することを意味する.例えば,
の値について収束することを意味する.例えば,![]() では次のようになる:
では次のようになる:
特性と関係 (11)
実数値数列については,DiscreteLimitが存在するならDiscreteMaxLimitはそれと同じ値になる:
DiscreteMaxLimitは常にDiscreteMinLimit以上である:
DiscreteMaxLimitとDiscreteMinLimitが等しいなら,その共通の値と等しい極限が存在する:
最大極限が![]() , なら,最小極限もそれに等しく,したがって極限もまた
, なら,最小極限もそれに等しく,したがって極限もまた![]() である:
である:
DiscreteMaxLimitは-DiscreteMinLimit[-f,…]として計算することができる:
この例のように2つの最大極限が等しいなら,![]() には極限がある:
には極限がある:
これは,はさみうちの定理 (またはサンドイッチ定理)の一般化である:
MaxLimitは常にDiscreteMaxLimit以上である:
考えられる問題 (1)
DiscreteMaxLimitは実数値数列に対してのみ定義される:
テキスト
Wolfram Research (2017), DiscreteMaxLimit, Wolfram言語関数, https://reference.wolfram.com/language/ref/DiscreteMaxLimit.html.
CMS
Wolfram Language. 2017. "DiscreteMaxLimit." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DiscreteMaxLimit.html.
APA
Wolfram Language. (2017). DiscreteMaxLimit. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DiscreteMaxLimit.html
BibTeX
@misc{reference.wolfram_2025_discretemaxlimit, author="Wolfram Research", title="{DiscreteMaxLimit}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/DiscreteMaxLimit.html}", note=[Accessed: 09-March-2026]}
BibLaTeX
@online{reference.wolfram_2025_discretemaxlimit, organization={Wolfram Research}, title={DiscreteMaxLimit}, year={2017}, url={https://reference.wolfram.com/language/ref/DiscreteMaxLimit.html}, note=[Accessed: 09-March-2026]}