DiscreteMaxLimit
DiscreteMaxLimit[f,k∞]
给出序列 f[k] 当 k 在整数上趋近于 ∞ 时的最大极限 k∞f(k).
DiscreteMaxLimit[f,{k1![]() ,…,kn
,…,kn![]() }]
}]
给出整数上的嵌套最大极限 ![]() ⋯
⋯ ![]() f(k1,…,kn).
f(k1,…,kn).
DiscreteMaxLimit[f,{k1,…,kn}{![]() ,…,
,…,![]() }]
}]
给出整数上的多变量最大极限 ![]() f(k1,…,kn).
f(k1,…,kn).
更多信息和选项



- DiscreteMaxLimit 亦称为 limit superior、supremum limit、limsup、upper limit 和 outer limit.
- DiscreteMaxLimit 计算极限的最小上限,且总是为实值序列定义. 它通常用于给出不依赖于实际极限的收敛条件和其他渐进属性.
- 可用
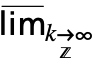 f 来输入 DiscreteMaxLimit[f,k∞]. 可用
f 来输入 DiscreteMaxLimit[f,k∞]. 可用  dMlim
dMlim 来输入模板
来输入模板 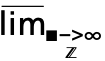 ,用
,用  把光标从底部移动到主体.
把光标从底部移动到主体. - 可用
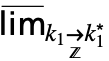 …
…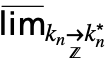 f 来输入 DiscreteMaxLimit[f,{k1,…,kn}{
f 来输入 DiscreteMaxLimit[f,{k1,…,kn}{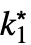 ,…,
,…, }].
}]. 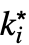 的极限值为 ±∞.
的极限值为 ±∞. - 最大极限被定义为最大包络序列 max[ω] 的极限:
-
DiscreteMaxLimit[f,k∞] DiscreteLimit[max[ω],ω∞] DiscreteMaxLimit[f,{k1,…,kn}{∞,…,∞}] DiscreteLimit[max[ω],ω∞] - DiscreteMaxLimit[f[k],k-∞] 等价于 DiscreteMaxLimit[f[-l],l∞] 等.
- 对单变量 f[k],定义使用最大包络 max[ω]MaxValue[{f[k],k≥ω∧k∈
 },k],对多变量 f[k1,…,kn],则使用 max[ω]MaxValue[{f[k1,…,kn],k1≥ω∧⋯∧kn≥ω∧ki∈
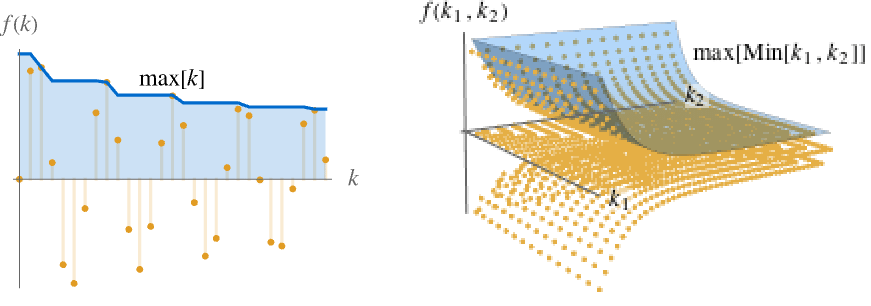
},k],对多变量 f[k1,…,kn],则使用 max[ω]MaxValue[{f[k1,…,kn],k1≥ω∧⋯∧kn≥ω∧ki∈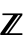 },{k1,…,kn}]. ω∞ 时,序列 max[ω] 单调递减,所以它总是有一个极限,可能是 ±∞.
},{k1,…,kn}]. ω∞ 时,序列 max[ω] 单调递减,所以它总是有一个极限,可能是 ±∞. - 下图中用蓝色显示 max[k] 和 max[Min[k1,k2]].
- 如果无法找到最大极限,DiscreteMaxLimit 不进行计算,直接返回.
- 可以给出下列选项:
-
Assumptions $Assumptions 对参数的假设 GenerateConditions Automatic 是否为参数生成条件 Method Automatic 所用的方法 PerformanceGoal "Quality" 优化的目标 - GenerateConditions 的可能设置包括:
-
Automatic 只汇报非通用条件 True 汇报所有条件 False 不汇报条件 None 如果需要条件,则不进行计算,直接返回 - PerformanceGoal 的可能设置包括 $PerformanceGoal、"Quality" 和 "Speed". 如果设置为 "Quality", DiscreteMaxLimit 通常能求解更多问题或产生更简单的结果,但会需要更多时间和内存.
范例
打开所有单元关闭所有单元基本范例 (4)
范围 (21)
特殊函数序列 (2)
选项 (6)
GenerateConditions (3)
当设置为 GenerateConditions->True 时,即便是非通用条件,也会汇报:
PerformanceGoal (1)
应用 (7)
基本应用 (2)
证明 DiscreteMaxLimit 和 DiscreteMinLimit 不相等:
用 DiscreteLimit 确认极限不存在:
级数收敛 (4)
用 DiscreteRatio 计算相邻项的比:
用 SumConvergence 确认级数是收敛的:
用 SumConvergence 确认级数是收敛的:
属性和关系 (11)
对于实值序列,如果 DiscreteLimit 存在,DiscreteMaxLimit 的值与之相等:
DiscreteMaxLimit 总是大于或等于 DiscreteMinLimit:
如果 DiscreteMaxLimit 等于 DiscreteMinLimit,极限存在并等于它们共有的值:
可用 -DiscreteMinLimit[-f,…] 来计算 DiscreteMaxLimit:
这是 "squeezing" 或 "sandwich" 定理的推广:
MaxLimit 总是大于或等于 DiscreteMaxLimit:
可能存在的问题 (1)
DiscreteMaxLimit 只对实值序列有定义:
文本
Wolfram Research (2017),DiscreteMaxLimit,Wolfram 语言函数,https://reference.wolfram.com/language/ref/DiscreteMaxLimit.html.
CMS
Wolfram 语言. 2017. "DiscreteMaxLimit." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/DiscreteMaxLimit.html.
APA
Wolfram 语言. (2017). DiscreteMaxLimit. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/DiscreteMaxLimit.html 年