E

自然対数の底を与え，その数値はとなる．

詳細

NumericQには数値として，Dには定数として扱われる数学定数である．
EはNを使って任意の数値精度で評価できる．
Eは，StandardFormとInputFormにおいて，，eeまたは\[ExponentialE]と入力することができる．
StandardFormとTraditionalFormにおいて，Eはと出力される．

予備知識

Eは，自然対数Logの底を表すシンボルである．また，オイラー数としても知られている．\[ExponentialE]で入力することができる．Eは，非負の整数の階乗の逆数の無限和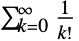として，あるいは極限値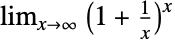として等，数学において数多くの同等の定義を持つ．Eは数値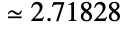を持つ．Piを以外では，Eはおそらく数学における最も重要な定数であり，多くの総和，積，積分，複利を含む式，指数関数的成長あるいは減衰を含む成長則，他の幅広い数学・科学分野の数式に見られる．
指数関数Exp[x]はE^x に変換される．Eがシンボルとして使用される場合は，厳密な数量として伝播される．Eを含む複雑な式の展開や簡約には，FunctionExpandやFullSimplifyのような関数が必要な場合がある．
オイラーはEが無理数である（2つの整数の比としては表せない）ことを証明し，続いてエルミートは，これが超越数である（整数多項式の根ではない）ことを立証した．しかし，Eは無理数度が2であるので，「可能な数の中で最も超越的ではない」数である．Eが任意の底で正規数である（b を底とした展開で各桁の数字が一様に分布している）かどうかは不明である．Eは，幅広い閉形式の総和や積分に見られるが，コンツェビッチ・ザギエ(Kontsevich-Zagier)周期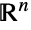（の代数的に指定された領域における有理係数を持つ一変量あるいは多変量の有理関数の絶対収束する積分の値ではない）ではないと推測されている．
EはNを使って任意の数値精度で評価することができる．事実，最新のデスクトップコンピュータを使うと，Eの最初の小数点以下百万桁の計算には1秒の数分の一しかかからない．RealDigitsを使ってEの各桁の数字のリストを，ContinuedFractionを使って連分数展開の項を得ることができる．