ElectrostaticPDEComponent

ElectrostaticPDEComponent[vars,pars]

静電気PDE項を，変数 vars，パラメータ pars で与える．

詳細

ElectrostaticPDEComponentは，通常，モデル変数 vars，モデルパラメータ pars で静電方程式を生成するために使用される．
ElectrostaticPDEComponentは，PDEの一部として使う微分演算子の和を返す．

ElectrostaticPDEComponentは，絶縁体または誘電体の材料内の静電荷によって生じる静電気場をモデル化する．

ElectrostaticPDEComponentは，静電気現象を，スカラー電位の従属変数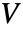でモデル化する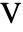．の単位はボルト[]，独立変数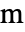の単位は[]である．
定常変数 vars は vars={V[x₁,…,x_n],{x₁,…,x_n}}である．
ElectrostaticPDEComponentは，一般に，時間依存編微分方程式は生成しない．
ElectrostaticPDEComponentは，拡散，ソース，PDEの導関数の各項に基づいている．

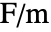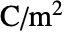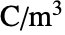は真空誘電率（単位：[]），破分局ベクトル（単位：[ $TemplateBox[{InterpretationBox[, 1], {"C", , "/", , {"m", ^, 2}}, coulombs per meter squared, {{(, "Coulombs", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]$ ] ），は体積電荷密度（単位：[ $TemplateBox[{InterpretationBox[, 1], {"C", , "/", , {"m", ^, 3}}, coulombs per meter cubed, {{(, "Coulombs", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]$ ]）である．
分極ベクトル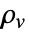は，材料内の永久または誘起電気双極子モーメントの密度を指定する．
体積電荷密度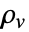は，正または負の電荷分布をモデル化する．
ElectrostaticPDEComponentは，構成関係によって異なる方程式を生成する．
ElectrostaticPDEComponentは，線形の材料については以下のように簡約される．

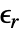は単位のない比誘電率である．
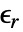は，等方性，直交異方性，異方性のいずれでもよい．
一般的な非線形で非ヒステリシスの強誘電体材料の場合，ElectrostaticPDEComponent方程式は以下として与えられる．

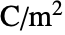は残留分極ベクトル（単位：[ $TemplateBox[{InterpretationBox[, 1], {"C", , "/", , {"m", ^, 2}}, coulombs per meter squared, {{(, "Coulombs", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]$ ]）である．
静電気モデルについての陰的なデフォルトの境界条件は0 ElectricFluxDensityValueである．
静電気モデル項の単位は[ $TemplateBox[{InterpretationBox[, 1], {"C", , "/", , {"m", ^, 3}}, coulombs per meter cubed, {{(, "Coulombs", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]$ ]あるいは同等の[ $TemplateBox[{InterpretationBox[, 1], {"s", , "A", , "/", , {"m", ^, 3}}, second amperes per meter cubed, {{(, {"Amperes", , "Seconds"}, )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]$ ]である．
次は，使用可能なパラメータ pars である．

パラメータ	デフォルト	シンボル
"Polarization"	{0,…}	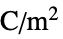，分極ベクトル（単位：[ $TemplateBox[{InterpretationBox[, 1], {"C", , "/", , {"m", ^, 2}}, coulombs per meter squared, {{(, "Coulombs", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]$ ]）
"RegionSymmetry"	None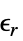
"RelativePermittivity"	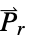	，無単位の比誘電率
"RemanentPolarization"	{0,…}	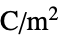，残留分極ベクトル（単位：[ $TemplateBox[{InterpretationBox[, 1], {"C", , "/", , {"m", ^, 2}}, coulombs per meter squared, {{(, "Coulombs", )}, /, {(, {"Meters", ^, 2}, )}}}, QuantityTF]$ ]）
"Thickness"	1	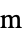，厚み（単位：[]）
"CrossSectionalArea"	1	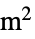，断面積（単位：[ $TemplateBox[{InterpretationBox[, 1], {{"m", ^, 2}}, meters squared, {"Meters", ^, 2}}, QuantityTF]$ ]）
"VacuumPermittivity"	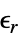	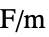，真空誘電率（単位：[]）
"VolumeChargeDensity"	0	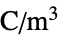，体積電荷密度（単位：[ $TemplateBox[{InterpretationBox[, 1], {"C", , "/", , {"m", ^, 3}}, coulombs per meter cubed, {{(, "Coulombs", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]$ ]）

パラメータはどれも，空間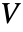変数と従属変数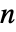に依存することがある．
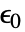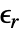独立変数の数はまたは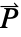の次元とベクトル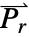および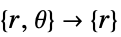の長さを決定する．
パラメータ"RegionSymmetry"の可能な選択肢には"Axisymmetric"がある．
"Axisymmetric"領域対称性は，以下のように角度変数を削除することによって円筒座標が縮小される，切り取られた円筒座標系を表す．
次元削減方程式

1D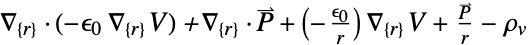

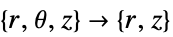
2D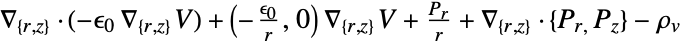
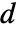
2Dの場合，"Thickness" が指定されているとElectrostaticPDEComponent方程式は以下のように与えられる．

1Dの場合，"CrossSectionalArea" 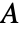が指定されているとElectrostaticPDEComponent方程式は以下のように与えられる．

1D軸対称の場合，"Thickness" 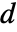が指定されると，ElectrostaticPDEComponent方程式は以下のように与えられる．

パラメータの入力指定は対応する演算子項のそれと厳密に等しい．
パラメータが指定されていない場合，デフォルトの静電気PDEは以下のようになる．

ElectrostaticPDEComponentが連想 pars で…,keyp_i…,p_iv_i,…]として指定されたパラメータ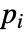に依存するとき，パラメータ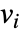は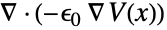で置換される．

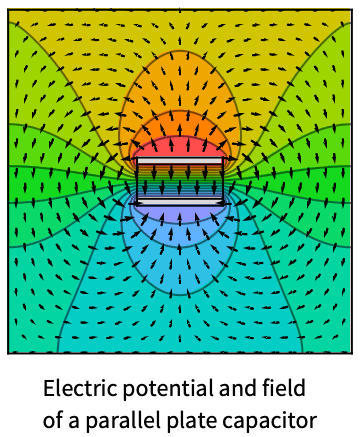
例題

すべて開くすべて閉じる

例 (3)

静電気モデルを定義する：

特定の材料パラメータで静電気モデルを設定する：

モデル変数と静電気パラメータを指定する：

静電気PDEを設定して解く：

解を可視化する：

スコープ (14)

1D (4)

断面積がの1D静電気モデルを定義する：

側面の2つの電位条件で電位場をモデル化する．

モデルの変数と静電パラメータを指定する：

線電気PDEを設定して解く：

解を可視化する：

側面における2つの電位条件と不連続比誘電率で電位場をモデル化する．

モデル変数と静電パラメータを指定する：

静電気PDEを設定して解く：

解を可視化する：

2D (5)

2D静電モデルを分極ベクトルで定義する：

2D非線形静電モデルを残留分極ベクトルで定義する：

2D静電モデルを厚みで定義する：

直交異方性比誘電率を定義する：

完全に異方性の比誘電率を定義する：

2D軸対称 (2)

2D軸対称静電気モデルを定義する：

2D軸対称直交静電モデルを定義する：

3D (1)

内半径と外半径の電位条件を使用して中空ボール内の電位場をモデル化する．

モデル変数と静電パラメータを指定する：

静電気PDEを設定して解く：

解を可視化する：

マルチマテリアル (2)

複数の材料領域について静電気モデルを設定する：

側面の2つの電位条件と不連続な比誘電率を持つ電位場をモデル化する．

モデル変数と静電パラメータを指定する：

静電気PDEを設定して解く：

解を可視化する：

アプリケーション (4)

1D (2)

距離 []で隔てられた軸に垂直の2枚の平行プレート間の電位分布を計算する．左側のパネルは定電位 []に保たれているのに対し，右側のプレートは接地していて []である．プレート間の領域は比誘電率と均一な電子電荷密度 [ $TemplateBox[{InterpretationBox[, 1], {"C", , "/", , {"m", ^, 3}}, coulombs per meter cubed, {{(, "Coulombs", )}, /, {(, {"Meters", ^, 3}, )}}}, QuantityTF]$ ]で特徴付られる．モデルの方程式は以下で与えられる：