Ellipsoid

Ellipsoid[p,{r1,…}]

中心が p で半軸の長さが riの，軸に沿った楕円体を表す．

Ellipsoid[p,Σ]

中心が p で，重み行列がΣでの楕円体を表す．

詳細とオプション

  • Ellipsoidは，中心区間，楕円，および超楕円体としても知られている．
  • Ellipsoidは，幾何学的領域およびグラフィックスプリミティブとして使うことが可能である．
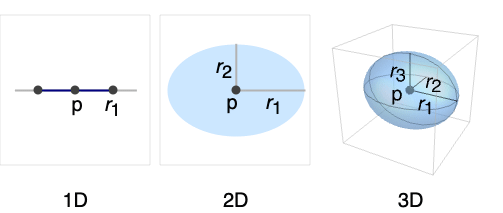
  • Ellipsoidは，軸に沿った，塗り潰された楕円体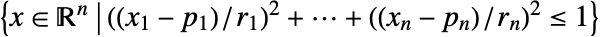，あるいは一般的な楕円体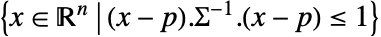を表す．
  • Ellipsoidでは，p は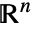の任意の点，riは正の実数，Σ は任意の対称正定実行列である．
  • Ellipsoidは，GraphicsおよびGraphics3Dで使うことができる．
  • グラフィックスでは，点 p，piおよび半径 riは，ScaledおよびDynamicの式でよい．
  • グラフィックスの描画はFaceForm，Specularity，Opacity，色等の指示子の影響を受ける．

例題

すべて開くすべて閉じる

例  (2)

3Dにおける軸に沿った楕円体：

2Dにおける：

測度と重心：

スコープ  (20)

グラフィックス  (10)

指定  (4)

3Dにおける軸に沿った楕円体：

2Dにおける：

3Dにおける一般的な楕円体：

2Dにおける：

スタイリング  (4)

さまざまな鏡面反射指数の球体：

赤く輝く黒い球体：

Opacityは表面の不透明度を指定する：

2Dのスタイリング：

座標  (2)

プロット範囲との割合で座標を指定する：

通常の座標からのスケールされたオフセットを指定する：

領域  (10)

埋込み次元は球体が存在する空間の次元である：

幾何次元は図形の次元である：

帰属判定：

点の帰属条件を求める：

体積：

重心：

点からの距離：

楕円の最近点までの距離：

点からの符号付きの距離：

楕円までの符号付きの距離：

領域内の最近点：

包み込んでいる球までの最近点：

楕円体は有界である：

その範囲を求める：

楕円体の領域で積分する：

楕円体の領域で最適化する：

楕円体の領域で方程式を解く：

アプリケーション  (4)

回転楕円体は，2本の等しい軸を持つ楕円体である：

その体積を計算する：

密度が で与えられる楕円体領域の総質量：

Ellipsoid内のメタノールの質量を求める：

メタノールの密度：

楕円体の体積：

楕円体内のメタノールの質量：

領域の境界ボックスに対しての，境界Ellipsoidを求める：

境界ボックスを計算する：

境界ボックスについての境界楕円体を計算する：

境界立体のVolumeの違いを計算する：

境界曲面を可視化する：

特性と関係  (4)

Diskは，Ellipsoidの特殊なケースである：

Ballは，Ellipsoidの特殊なケースである：

Ellipsoidは，Ballを一般化したものである：

ImplicitRegionは，任意のEllipsoidを表すことができる：

おもしろい例題  (2)

ランダムな楕円体の集合：

軸の周りで楕円体を急速に動かす：

Wolfram Research (2014), Ellipsoid, Wolfram言語関数， https://reference.wolfram.com/language/ref/Ellipsoid.html.

テキスト

Wolfram Research (2014), Ellipsoid, Wolfram言語関数， https://reference.wolfram.com/language/ref/Ellipsoid.html.

CMS

Wolfram Language. 2014. "Ellipsoid." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Ellipsoid.html.

APA

Wolfram Language. (2014). Ellipsoid. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Ellipsoid.html

BibTeX

@misc{reference.wolfram_2024_ellipsoid, author="Wolfram Research", title="{Ellipsoid}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/Ellipsoid.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_ellipsoid, organization={Wolfram Research}, title={Ellipsoid}, year={2014}, url={https://reference.wolfram.com/language/ref/Ellipsoid.html}, note=[Accessed: 21-November-2024 ]}