ExponentialFamily

ExponentialFamily

is an option for GeneralizedLinearModelFit that specifies the exponential family for the model.

Details

  • ExponentialFamily specifies the assumed distribution for the independent 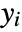observations modeled by .
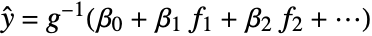  • The density function for an exponential family can be written in the form 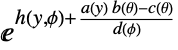for functions 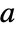, , 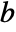, , 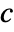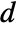and 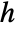, random variable 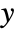, canonical parameter 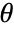, and dispersion parameter .
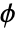  • Possible parametric distributions include: "Binomial", "Poisson", "Gamma", "Gaussian", "InverseGaussian".
  • The observed responses 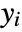are restricted to the domains of parametric distributions as follows:
  • "Binomial"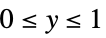
    "Gamma"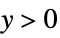
    "Gaussian"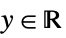
    "InverseGaussian"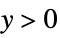
    "Poisson"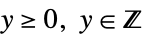
  • The setting ExponentialFamily->"QuasiLikelihood", defines a quasi-likelihood function, used for a maximum likelihood fit.
  • The log quasi-likelihood function for the response 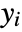and prediction 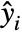is given by 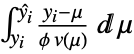, where 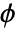is the dispersion parameter and 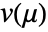is the variance function. The dispersion parameter is estimated from input data and can be controlled through the option DispersionEstimatorFunction.
  • The setting ExponentialFamily->{"QuasiLikelihood",opts} allows the following quasi-likelihood suboptions to be specified:
  • "ResponseDomain"Function[y,y>0]domain for responses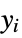
    "VarianceFunction"Function[μ,1]variance as function of mean
  • The parametric distributions can be emulated with quasi-likelihood structures by using the following "VarianceFunction" and "ResponseDomain" suboption settings:
  • "Binomial"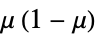0<=y<=1
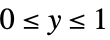
    "Gamma"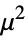
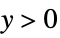
    "Gaussian"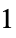
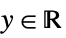
    "InverseGaussian"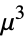
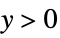
    "Poisson"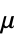
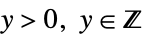
  • "QuasiLikelihood" variants of "Binomial" and "Poisson" families can be used to model overdispersed (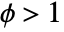) or underdispersed (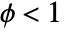) data, different from the theoretical dispersion ().
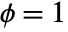  • Common variance functions, response domains, and uses include:
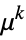
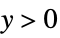
  • power models, actuarial science, meteorology, etc.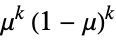
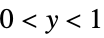
    probability models, binomial related, etc.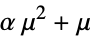
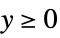
    counting models, Poisson related, etc.

Examples

open allclose all

Basic Examples  (1)

Fit data to a simple linear regression model:

Fit to a canonical gamma regression model:

Fit to a canonical inverse Gaussian regression model:

Scope  (2)

Use the "Binomial" family for logit models of probabilities:

Use "Poisson" for log‐linear models of count data:

Properties & Relations  (3)

The default ExponentialFamily and LinkFunction match LinearModelFit:

The default "Binomial" model matches LogitModelFit:

Fit a "Gamma" model and the "QuasiLikelihood" analog:

The models differ from named analogs by a constant in the "LogLikelihood":

Fitted parameters agree:

Results based on differences of log-likelihoods agree:

Wolfram Research (2008), ExponentialFamily, Wolfram Language function, https://reference.wolfram.com/language/ref/ExponentialFamily.html.

Text

Wolfram Research (2008), ExponentialFamily, Wolfram Language function, https://reference.wolfram.com/language/ref/ExponentialFamily.html.

CMS

Wolfram Language. 2008. "ExponentialFamily." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ExponentialFamily.html.

APA

Wolfram Language. (2008). ExponentialFamily. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ExponentialFamily.html

BibTeX

@misc{reference.wolfram_2025_exponentialfamily, author="Wolfram Research", title="{ExponentialFamily}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/ExponentialFamily.html}", note=[Accessed: 21-February-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_exponentialfamily, organization={Wolfram Research}, title={ExponentialFamily}, year={2008}, url={https://reference.wolfram.com/language/ref/ExponentialFamily.html}, note=[Accessed: 21-February-2025 ]}