DispersionEstimatorFunction

✖
`DispersionEstimatorFunction`

✖

DispersionEstimatorFunction

is an option for generalized linear model fitting functions that specifies the estimator for the dispersion parameter.

Details

DispersionEstimatorFunction is an option for GeneralizedLinearModelFit, LogitModelFit, and ProbitModelFit.
With DispersionEstimatorFunction->"PearsonChiSquare", the estimator is 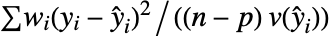where 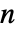is the number of data points, 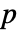is the number of parameters, and 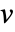is the variance function for the distribution.
With DispersionEstimatorFunction->Automatic, the following estimates are used:
"Binomial" 1

"Gamma"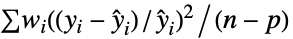

"Gaussian"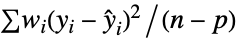

"InverseGaussian"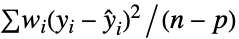

"Poisson" 1

"QuasiLikelihood"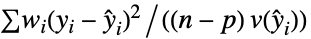
Non‐default values can be used to model overdispersion in "Binomial" and "Poisson" models.
With the setting DispersionEstimatorFunction->f, the common dispersion is estimated by f[y,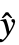,w] where y={y₁,y₂,…} is the list of observations, 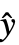={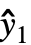,,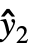…} is the list of predicted values, and w={w₁,w₂,…} is the list of weights for the measurements y_i.

Examples

open allclose all

Basic Examples (1)Summary of the most common use cases

Fit a Poisson model:

In[1]:=1

✖

https://wolfram.com/xid/0bmukxikm8pdj0rl3de-brkjy3

In[2]:=2

✖

https://wolfram.com/xid/0bmukxikm8pdj0rl3de-crq2bc

Out[2]=2

Compute the covariance matrix using the default dispersion estimate:

In[3]:=3

✖

https://wolfram.com/xid/0bmukxikm8pdj0rl3de-ks68gb

Out[3]=3

Estimate the dispersion by Pearson's :

In[4]:=4

✖

https://wolfram.com/xid/0bmukxikm8pdj0rl3de-jt4pb7

Out[4]=4

Estimate the dispersion by the mean squared error:

In[5]:=5

✖

https://wolfram.com/xid/0bmukxikm8pdj0rl3de-dyzon

Out[5]=5

Scope (2)Survey of the scope of standard use cases

Define the estimate within the FittedModel:

In[1]:=1

✖

https://wolfram.com/xid/0bmukxikm8pdj0rl3de-evc252

In[2]:=2

✖

https://wolfram.com/xid/0bmukxikm8pdj0rl3de-cnz99m

Out[2]=2

In[3]:=3

✖

https://wolfram.com/xid/0bmukxikm8pdj0rl3de-jj6u3j

Out[3]=3

In[4]:=4

✖

https://wolfram.com/xid/0bmukxikm8pdj0rl3de-em28ru

Out[4]=4

In[5]:=5

✖

https://wolfram.com/xid/0bmukxikm8pdj0rl3de-c7pfx

Out[5]=5

In[6]:=6

✖

https://wolfram.com/xid/0bmukxikm8pdj0rl3de-eykbej

Out[6]=6

Fit a logit model:

In[1]:=1

✖

https://wolfram.com/xid/0bmukxikm8pdj0rl3de-kbjbsx

In[2]:=2

✖

https://wolfram.com/xid/0bmukxikm8pdj0rl3de-gs9gof

Out[2]=2

Estimate the dispersion by the sum of squared errors:

In[3]:=3

✖

https://wolfram.com/xid/0bmukxikm8pdj0rl3de-ddagjx

Out[3]=3

Fit a probit model:

In[4]:=4

✖

https://wolfram.com/xid/0bmukxikm8pdj0rl3de-gmg7i8

Out[4]=4

Estimate the dispersion by the mean squared error:

In[5]:=5

✖

https://wolfram.com/xid/0bmukxikm8pdj0rl3de-inm1og

Out[5]=5

Top