VarianceEstimatorFunction

VarianceEstimatorFunction

is an option for LinearModelFit and NonlinearModelFit which specifies the variance estimator to use.

Details

  • VarianceEstimatorFunction defines the function for estimating the error variance scale for linear and nonlinear models with assumed normally distributed errors.
  • With the setting VarianceEstimatorFunction->f, the variance scale is estimated by f[res,w] where res={y1-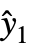,y2-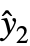,…} is the list of residuals and w is the list of weights, as specified by the setting for the Weights option.
  • The default setting Automatic estimates the variance scale by 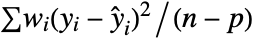where 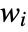is the weight for the 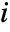th data point, 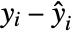is the 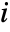th residual, 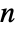is the number of data elements, and 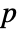is the number of parameters in the model.
  • With VarianceEstimatorFunction->(1&) and Weights->{1/Δy12,1/Δy22,…}, Δyi is treated as the known uncertainty of measurement yi and parameter standard errors are effectively computed only from the weights. »

Examples

open allclose all

Basic Examples  (1)

Use the default unbiased estimate of error variance:

Assume a known error variance:

Estimate the variance by the mean squared error:

Scope  (2)

Define the estimate within the FittedModel:

Use with a nonlinear model:

Estimate the variance by the mean absolute error:

Applications  (1)

Fit a nonlinear model using measurement errors as weights:

Estimate the common error scale by 1:

Obtain standard errors for the parameters:

Compare with estimates using the default variance estimate:

Properties & Relations  (1)

Error estimates and confidence intervals involve variance estimates:

Use the default estimator:

Assume unit error scale:

Estimate by mean squared error:

Wolfram Research (2008), VarianceEstimatorFunction, Wolfram Language function, https://reference.wolfram.com/language/ref/VarianceEstimatorFunction.html.

Text

Wolfram Research (2008), VarianceEstimatorFunction, Wolfram Language function, https://reference.wolfram.com/language/ref/VarianceEstimatorFunction.html.

CMS

Wolfram Language. 2008. "VarianceEstimatorFunction." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/VarianceEstimatorFunction.html.

APA

Wolfram Language. (2008). VarianceEstimatorFunction. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/VarianceEstimatorFunction.html

BibTeX

@misc{reference.wolfram_2024_varianceestimatorfunction, author="Wolfram Research", title="{VarianceEstimatorFunction}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/VarianceEstimatorFunction.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_varianceestimatorfunction, organization={Wolfram Research}, title={VarianceEstimatorFunction}, year={2008}, url={https://reference.wolfram.com/language/ref/VarianceEstimatorFunction.html}, note=[Accessed: 21-November-2024 ]}