FindHamiltonianCycle

FindHamiltonianCycle[g]

グラフ g のハミルトン(Hamilton)閉路を求める．

FindHamiltonianCycle[g,k]

最大 k 個のハミルトン閉路を求める．

FindHamiltonianCycle[{vw,…},…]

規則 vw を使ってグラフ g を指定する．

詳細とオプション

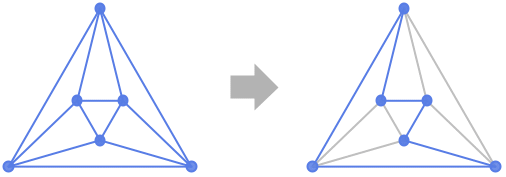
予備知識

  • FindHamiltonianCycle は，他と区別できる1つ以上のハミルトン(Hamilton)閉路（ハミルトン回路と呼ばれることもある）を見付けようと試みる．ハミルトン閉路は，辺リストのリストとして，あるいは見付からない場合には{}として返される．ハミルトン閉路（閉路が特定の端点を持つ明示的な経路を使って識別される場合には，より正しくはハミルトン回路と呼ばれる）は，最初と最後の辺が端点で繋がり，各頂点が厳密に1度だけ現れるような，互いに区別の付く辺の連続する列である．このため，ハミルトン閉路は，長さ 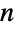のグラフ閉路である．ここで 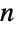は，グラフ内のノードの数である．ハミルトン閉路は，ゲノム配列を再構築したり，ゲーム（ハミルトンの世界一周ゲーム(Icosian Game)が最も有名）を解いたり，チェス盤上のナイトの巡回を求めたり，正規グラフの魅力的な円状の埋込みを求めたりするのに使われる．ハミルトン閉路を含むグラフはハミルトングラフとして知られる．
  • FindHamiltonianCycle[g,k]は，k 個のハミルトン回路を求めようと試みる．回数指定 k は省略する（その場合には1であるとみなされる）場合も，正の整数の場合も，あるいはAllになる場合もある．
  • ハミルトン閉路を求めることは，NP完全問題である．しかし，ハミルトン閉路を非常に素早く求めることができる（ただしいつもそうであるとは限らない）さまざまな発見的アルゴリズムが存在する．このことから，グラフ内の頂点を置換するだけで，FindHamiltonianCycleのランタイムが異なる場合がある．
  • グラフがハミルトン経路かどうかはHamiltonianGraphQを使って調べることができる．FindShortestTourは，グラフ（より一般的にいうなら指定された頂点集合）上の単一のハミルトン経路を求めようと試みる別の関数である．この関数はFindHamiltonianCycleよりも速く成功することがある点で有利である．
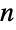  • 個のノードを持つグラフ内のハミルトン閉路は，長さ 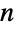の閉路に対応するが，任意長の閉路はFindCycleを使って求められる場合がある．ハミルトン閉路はすべての頂点を訪れるが，すべての辺を通るとは限らない．すべての辺を厳密に1度だけ通る閉路は，オイラー(Euler)回路であり，FindEulerianCycleを使って求めることができる．

例題

すべて開くすべて閉じる

例  (2)

ハミルトン閉路を求める：

閉路を示す：

いくつかのハミルトン閉路を求める：

スコープ  (8)

FindHamiltonianCycleは無向グラフに使うことができる：

有向グラフにも使うことができる：

多重グラフ：

混合グラフ：

いくつかのハミルトン閉路を求める：

規則を使ってグラフを指定する：

FindHamiltonianCycleはハミルトングラフではないものに対しては空の結果を返す：

FindHamiltonianCycleは大きいグラフに使うことができる：

アプリケーション  (5)

十二面体の辺に沿ったハミルトン閉路を見付けることで「Icosian game [MathWorld]」を解く：

ラベル付きの12面体上で指定したラベルの列を含むハミルトン閉路を求める：

B, C, P, N, Mという文字列を含む閉路を求める：

閉路をハイライトする：

8×8のチェス盤のそれぞれの升目を厳密に1回ずつ訪れる一続きのチェスのナイトの動きがあるかどうか調べる：

騎士の周遊：

頂点が長さ k の部分配列で辺がペアワイズアライメントの，環状ゲノムのグラフに基づいたアセンブリ"ATGGCGTGCA"：

ゲノムを再構成する：

位数 のグレーコードは超立方体グラフ のハミルトン閉路である：

のすべてのハミルトン閉路を求める：

グレーコードをハイライトする：

特性と関係  (5)

ハミルトングラフの大規模なコレクションを得るのにGraphDataを使う：

非ハミルトングラフ：

HamiltonianGraphQを使って，グラフにハミルトン閉路が含まれるかどうかを確かめる：

ハミルトングラフは二重連結している：

ハミルトングラフの線グラフにはハミルトン閉路が含まれる：

オイラーグラフの線グラフにはハミルトン閉路が含まれる：

個の頂点を持ち最小次数がより大きい無向グラフにはハミルトン閉路が含まれる：

個の頂点を持ち最小次数が より大きい有向グラフにはハミルトン閉路が含まれる：

おもしろい例題  (1)

ハミルトン閉路を求める：

閉路を動的にハイライトする：

Wolfram Research (2010), FindHamiltonianCycle, Wolfram言語関数， https://reference.wolfram.com/language/ref/FindHamiltonianCycle.html （2015年に更新）.

テキスト

Wolfram Research (2010), FindHamiltonianCycle, Wolfram言語関数， https://reference.wolfram.com/language/ref/FindHamiltonianCycle.html （2015年に更新）.

CMS

Wolfram Language. 2010. "FindHamiltonianCycle." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/FindHamiltonianCycle.html.

APA

Wolfram Language. (2010). FindHamiltonianCycle. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FindHamiltonianCycle.html

BibTeX

@misc{reference.wolfram_2024_findhamiltoniancycle, author="Wolfram Research", title="{FindHamiltonianCycle}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/FindHamiltonianCycle.html}", note=[Accessed: 14-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_findhamiltoniancycle, organization={Wolfram Research}, title={FindHamiltonianCycle}, year={2015}, url={https://reference.wolfram.com/language/ref/FindHamiltonianCycle.html}, note=[Accessed: 14-November-2024 ]}