Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

ForAll

ForAll[x,expr]

represents the statement that expr is True for all values of .

ForAll[x,cond,expr]

states that expr is True for all x satisfying the condition cond.

ForAll[{x₁,x₂,…},expr]

states that expr is True for all values of all the x_i.

Details

ForAll[x,expr] can be entered as ∀_xexpr. The character ∀ can be entered as fa or \[ForAll]. The variable x is given as a subscript.
ForAll[x,cond,expr] can be entered as ∀_x,condexpr.
In StandardForm, ForAll[x,expr] is output as ∀_xexpr.
ForAll[x,cond,expr] is output as ∀_x,condexpr.
ForAll can be used in such functions as Reduce, Resolve, and FullSimplify.
The condition cond is often used to specify the domain of a variable, as in x∈Integers.
ForAll[x,cond,expr] is equivalent to ForAll[x,Implies[cond,expr]].
ForAll[{x₁,x₂,…},…] is equivalent to .
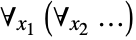The value of 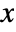in ForAll[x,expr] is taken to be localized, as in Block.

Examples

open allclose all

Basic Examples (1)

This states that for all , is positive:

Use Resolve to get a condition on real parameters for which the statement is true:

Reduce gives the condition in a solved form:

Scope (6)

This states that for all the inequation is true:

Use Resolve to prove that the statement is false:

This states that for all real the inequation is true:

Use Resolve to prove that the statement is true:

This states that for all pairs the inequality is true:

With domain not specified, Resolve considers algebraic variables in inequalities to be real:

With domain Complexes, complex values that make the inequality False are allowed:

This states the tautology implies :

Prove it:

If the expression does not explicitly contain a variable, ForAll simplifies automatically:

TraditionalForm formatting:

Applications (5)

This states the inequality between the arithmetic mean and the geometric mean:

Use Resolve to prove the inequality:

This states a special case of Hölder's inequality:

Use Resolve to prove the inequality:

This states a special case of Minkowski's inequality:

Use Resolve to prove the inequality:

Prove geometric inequalities for , , and sides of a triangle:

This states that an inequality is satisfied for all triangles:

Use Resolve to prove the inequality:

This states that an inequality is satisfied for all acute triangles:

Use Resolve to prove the inequality:

Test whether one region is included in another:

This states that all points satisfying R1 also satisfy R2:

The statement is true, hence the region defined by R1 is included in the region defined by R2:

Plot the relationship:

Properties & Relations (3)

Negation of ForAll gives Exists:

Quantifiers can be eliminated using Resolve or Reduce:

This eliminates the quantifier:

This eliminates the quantifier and solves the resulting equations and inequalities:

This states that an equation is true for all complex values of :

Use Reduce to find the values of parameters for which the statement is true:

This solves the same problem using SolveAlways:

Top