ForAll 
更多信息

- ForAll[x,expr] 可以输入为 ∀xexpr 的形式. 字符 ∀ 可以通过输入
 fa
fa 或 \[ForAll] 获得. 变量 x 可以以下标形式给出.
或 \[ForAll] 获得. 变量 x 可以以下标形式给出. - ForAll[x,cond,expr] 可以输入为 ∀x,condexpr 的形式.
- 在 StandardForm 中,ForAll[x,expr] 输出为 ∀xexpr.
- ForAll[x,cond,expr] 输出为 ∀x,condexpr.
- ForAll 可以用于诸如 Reduce、Resolve 和 FullSimplify 的函数中.
- 条件 cond 通常用于指定一个变量的域,例如 x∈Integers.
- ForAll[x,cond,expr] 等价于 ForAll[x,Implies[cond,expr]].
- ForAll[{x1,x2,…},…] 等价于
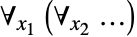 .
. - ForAll[x,expr] 中的
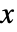 值一般采用局部化,例如 Block.
值一般采用局部化,例如 Block.
范例
打开所有单元关闭所有单元范围 (6)
应用 (5)
Wolfram Research (2003),ForAll,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ForAll.html.
文本
Wolfram Research (2003),ForAll,Wolfram 语言函数,https://reference.wolfram.com/language/ref/ForAll.html.
CMS
Wolfram 语言. 2003. "ForAll." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/ForAll.html.
APA
Wolfram 语言. (2003). ForAll. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ForAll.html 年