FourierDST

FourierDST[list]

実数リストの離散フーリエ(Fourier)正弦変換を求める．

FourierDST[list,m]

タイプ の離散フーリエ正弦変換を求める．

詳細

  • 長さ 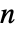のリスト 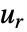についての結果 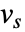を返す離散フーリエ正弦変換の可能なタイプ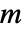
  • 1 (DST-I)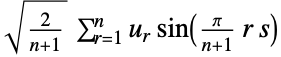
    2 (DST-II)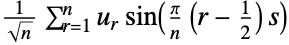
    3 (DST-III)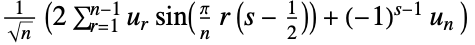
    4 (DST-IV)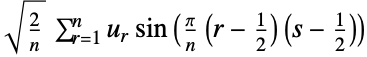
  • FourierDST[list]はFourierDST[list,2]に等しい．
  • タイプ1，2，3，4の離散フーリエ正弦変換の逆変換は，それぞれタイプ1，3，2，4である．
  • FourierDST[list]で与えられる list は，任意次元のデータ配列を表すようにネストしていてもよい．
  • データ配列は長方形でなければならない．
  • list 中の要素が厳密数の場合，FourierDSTはNを適用することから始める．
  • FourierDSTはSparseArrayオブジェクトに使うことができる．

例題

すべて開くすべて閉じる

例  (2)

離散正弦変換を求める：

離散正弦変換の逆変換を求める：

タイプ1(DST-I)の離散正弦変換を求める：

離散正弦変換の逆変換を求める：

スコープ  (2)

機械演算を使って離散正弦変換を計算する：

24桁精度演算を使う：

二次元離散正弦変換：

四次元離散正弦変換：

一般化と拡張  (2)

このリストは複素数値を持つかもしれない：

タイプ1，2，3，4に，順に"I"，"II"，"III"，"IV"を用いてもよい：

アプリケーション  (2)

正弦級数展開  (1)

正弦の総和としての奇関数についての展開を求める：

[-L,L)上の n 個の点を持つ等間隔の格子上の関数の値：

DST-Iを計算し，再正規化する：

この関数は，実質的に，特定の奇対称で期分けされている：

点が定義されているところの展開誤差をプロットする：

擬スペクトルPDE離散化  (1)

二次導関数を境界条件が零個の関数について近似する：

波動方程式を撥弦について解く：

解 を曲面としてプロットする：

特性と関係  (3)

DST-IとDST-IVは互いに逆関数である：

DST-IIとDST-IIIは互いに逆関数である：

DSTは行列の乗算に等しい：

考えられる問題  (1)

FourierDSTは，常に正規化された結果を返す：

正規化されていない結果を求めるのには，正規化で乗算する：

Wolfram Research (2007), FourierDST, Wolfram言語関数， https://reference.wolfram.com/language/ref/FourierDST.html.

テキスト

Wolfram Research (2007), FourierDST, Wolfram言語関数， https://reference.wolfram.com/language/ref/FourierDST.html.

CMS

Wolfram Language. 2007. "FourierDST." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FourierDST.html.

APA

Wolfram Language. (2007). FourierDST. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FourierDST.html

BibTeX

@misc{reference.wolfram_2024_fourierdst, author="Wolfram Research", title="{FourierDST}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/FourierDST.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_fourierdst, organization={Wolfram Research}, title={FourierDST}, year={2007}, url={https://reference.wolfram.com/language/ref/FourierDST.html}, note=[Accessed: 17-November-2024 ]}