FourierDST

FourierDST[list]

求实数列表的傅立叶离散正弦变换.

FourierDST[list,m]

求类型 的傅立叶离散正弦变换.

更多信息

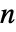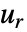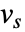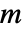  • 长度为 的列表 的离散正弦变换给出的结果为 的可能类型 是：
  • 1 (DST-I)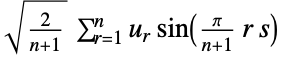
    2 (DST-II)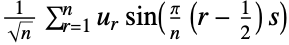
    3 (DST-III)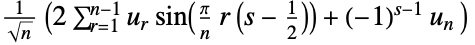
    4 (DST-IV)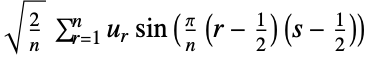
  • FourierDST[list] 等价于 FourierDST[list,2].
  • 类型为 1，2，3，4 的逆离散正弦变换的类型分别为 1，3，2，4.
  • FourierDST[list] 中的 list 可以被嵌套来表示任意维度的数据数组.
  • 数据数组必须是长方形.
  • 如果 list 的元素是确切的数字，则 FourierDST 首先应用 N.
  • FourierDST 可用于 SparseArray 对象.

范例

打开所有单元关闭所有单元

基本范例  (2)

求一个离散正弦变换：

求离散正弦逆变换：

求类型1（DST-I ）的离散正弦变换：

求离散正弦逆变换：

范围  (2)

使用机器精度计算离散正弦变换：

使用24位精度计算：

二维离散正弦变换：

四维离散正弦变换：

推广和延伸  (2)

此列表有复数值：

您可以使用 "I"，"II"，"III"，或 "IV" 代表型 1，2，3，和 4：

应用  (2)

正弦级数展开  (1)

获得奇函数的展开作为正弦的和：

在均匀间隔的网格上的函数值是在 [-L,L) 区间内的 n 个点：

计算 DST-I 并正规化：

该函数，实际上被周期化，且具有奇对称性：

在定义点处绘制展开误差：

拟谱偏微分方程离散化  (1)

函数在零边界条件下的二阶近似导数：

求解采集串的波动方程：

以 的解作为表面的图形：

属性和关系  (3)

DST-I 和 DST-IV 是它们自己的逆：

DST-II 和 DST-III 互为逆：

DST 等效于矩阵乘法：

可能存在的问题  (1)

FourierDST 总是返回正规化结果：

您可以乘以一个正规化结果得到非正规化结果：

Wolfram Research (2007)，FourierDST，Wolfram 语言函数，https://reference.wolfram.com/language/ref/FourierDST.html.

文本

Wolfram Research (2007)，FourierDST，Wolfram 语言函数，https://reference.wolfram.com/language/ref/FourierDST.html.

CMS

Wolfram 语言. 2007. "FourierDST." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/FourierDST.html.

APA

Wolfram 语言. (2007). FourierDST. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/FourierDST.html 年

BibTeX

@misc{reference.wolfram_2024_fourierdst, author="Wolfram Research", title="{FourierDST}", year="2007", howpublished="\url{https://reference.wolfram.com/language/ref/FourierDST.html}", note=[Accessed: 17-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_fourierdst, organization={Wolfram Research}, title={FourierDST}, year={2007}, url={https://reference.wolfram.com/language/ref/FourierDST.html}, note=[Accessed: 17-November-2024 ]}