FunctionSingularities
![]() の特異点を x∈Realsについて求める.
の特異点を x∈Realsについて求める.
FunctionSingularities[f,x,dom]
![]() の特異点を x∈dom について求める.
の特異点を x∈dom について求める.
FunctionSingularities[{f1,f2,…},{x1,x2,…},dom]
![]() の特異点を x1,x2,…∈dom について求める.
の特異点を x1,x2,…∈dom について求める.
詳細


- 関数の特異点は,通常は,関数が解析的であることが保証されている領域を見付けるためまたは特別な解析を実行する必要がある点と曲線を見付けるために使用される.
- FunctionSingularitiesは,
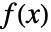 が
が 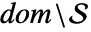 で解析できるように,集合
で解析できるように,集合 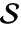 の暗黙の記述を与える.集合
の暗黙の記述を与える.集合 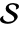 は最小であるとは限らない.
は最小であるとは限らない. - 結果として得られる暗黙の記述は,等式,不等式,領域指定,およびこれらの論理結合で構成され,ReduceやSolve等の関数での使用に適している.
- ローラン(Laurent)級数表現,多変量関数,関数の区分的および部分的な定義等,特異点のソースはいくつかある.
- 次は,
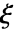 が孤立特異点の位置を示す,ローラン級数表現
が孤立特異点の位置を示す,ローラン級数表現 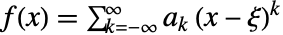 からの特異点である.
からの特異点である. -
可除特異点 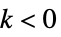 について
について 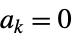 ,つまり,
,つまり,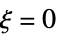 について
について 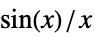
極特異点 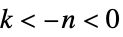 について
について 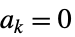 ,つまり,
,つまり,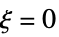 について
について 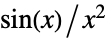
真性特異点 無限に多くの 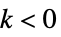 について
について 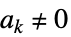 ,つまり,
,つまり,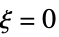 について
について 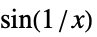
非真性特異点 極または可除特異点 - 次は,多変量関数の分岐点の選択からの特異点である.
-
分岐点 多変量関数の分枝が一緒になる点,つまり, 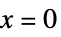 について
について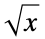
分枝 単一の値となるために関数がそれに沿って不連続となる曲線,つまり, 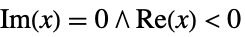 について
について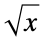
- 次は,区分的に定義された関数あるいは定義の自然領域からの特異点である.
-
区分的 区分的に定義された関数,つまり, 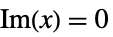 について
について 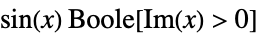
定義領域 定義領域の補領域,つまり, ![TemplateBox[{x}, Abs]>=1 TemplateBox[{x}, Abs]>=1](Files/FunctionSingularities.ja/28.png) について
について ![TemplateBox[{1, {1, /, 2}, x}, EllipticTheta] TemplateBox[{1, {1, /, 2}, x}, EllipticTheta]](Files/FunctionSingularities.ja/29.png)
- 多変量関数については,特異点は各変数の個別の特異点であるとみなされる.
- dom の可能な値はRealsおよびComplexesである.
例題
すべて開くすべて閉じるスコープ (5)
アプリケーション (6)
基本的なアプリケーション (5)
特性と関係 (3)
この関数は,FunctionSingularitiesで与えられる集合の外側では解析的である:
FunctionAnalyticを使って解析性を検証する:
FunctionDiscontinuitiesは,関数がその外側では連続的になる集合を与える:
FunctionSingularitiesはすべての特異点が満足する条件を求める:
SolveValuesを使って特異点を求める:
FunctionPolesを使って極特異点とその多重度を求める:
テキスト
Wolfram Research (2020), FunctionSingularities, Wolfram言語関数, https://reference.wolfram.com/language/ref/FunctionSingularities.html.
CMS
Wolfram Language. 2020. "FunctionSingularities." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/FunctionSingularities.html.
APA
Wolfram Language. (2020). FunctionSingularities. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/FunctionSingularities.html