WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

GaussianIntegers

FactorInteger，PrimeQ，Factor等の関数に与えるオプションで，ガウス整数の添加された整数環上で因数分解がなされるかどうかを指定する．

詳細
Details and Options Details and Options
例題  
例  
スコープ  
特性と関係  
関連項目
テクニカルノート
関連するガイド
履歴
引用書式

GaussianIntegers

GaussianIntegers

FactorInteger，PrimeQ，Factor等の関数に与えるオプションで，ガウス整数の添加された整数環上で因数分解がなされるかどうかを指定する．

詳細

  • GaussianIntegers->Falseの設定では，通常の整数環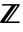上で因数分解が行われる．
  • GaussianIntegers->Trueの設定では，ガウス整数（虚数単位）i の添加された整数環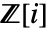上で因数分解が行われる．
  • GaussianIntegers->Trueの設定では，実部・虚部がともに正となるようなガウスの素数が使われる．
  • GaussianIntegers->Trueの設定では，FactorIntegerが与えるリストの第1要素は-1または-Iとなる．

例題

すべて開く すべて閉じる

例  (1)

上で多項式を因数分解する：

Wolfram Language code: Factor[x ^ 2 + 1, GaussianIntegers -> True]

上で整数を因数分解する：

Wolfram Language code: FactorInteger[2, GaussianIntegers -> True]

スコープ  (3)

デフォルトで，多項式の因数分解は有理数上で行われる：

Wolfram Language code: Factor[x ^ 4 - 16]

次は，上で因数分解を行うように指定する：

Wolfram Language code: Factor[x ^ 4 - 16, GaussianIntegers -> True]

デフォルトで，整数の因数分解は整数上で行われる：

Wolfram Language code: FactorInteger[12]

次は，因数分解をガウス整数上で行うように指定する：

Wolfram Language code: FactorInteger[12, GaussianIntegers -> True]

整数上の素数はガウス整数上では素数ではないことがある：

Wolfram Language code: PrimeQ[17]
Wolfram Language code: PrimeQ[17, GaussianIntegers -> True]

特性と関係  (1)

Factorにとって，GaussianIntegers->TrueはExtension->Iに等しい：

Wolfram Language code: Factor[x ^ 4 + 1, GaussianIntegers -> True]
Wolfram Language code: Factor[x ^ 4 + 1, Extension -> I]
Wolfram Research (1991), GaussianIntegers, Wolfram言語関数， https://reference.wolfram.com/language/ref/GaussianIntegers.html.

テキスト

Wolfram Research (1991), GaussianIntegers, Wolfram言語関数， https://reference.wolfram.com/language/ref/GaussianIntegers.html.

CMS

Wolfram Language. 1991. "GaussianIntegers." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/GaussianIntegers.html.

APA

Wolfram Language. (1991). GaussianIntegers. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GaussianIntegers.html

BibTeX

@misc{reference.wolfram_2026_gaussianintegers, author="Wolfram Research", title="{GaussianIntegers}", year="1991", howpublished="\url{https://reference.wolfram.com/language/ref/GaussianIntegers.html}", note=[Accessed: 08-November-2026]}

BibLaTeX

@online{reference.wolfram_2026_gaussianintegers, organization={Wolfram Research}, title={GaussianIntegers}, year={1991}, url={https://reference.wolfram.com/language/ref/GaussianIntegers.html}, note=[Accessed: 08-November-2026]}