GeneralizedPower
GeneralizedPower[f,x,k]
Details
- GeneralizedPower is used to represent an integer power of a binary operation.
- If f has the Flat attribute, GeneralizedPower[f,x,k] is equivalent to f[
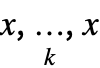]. - GeneralizedPower[f,x,k] is typeset as
.
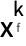Examples
open all close allBasic Examples (1)
Represent the third power of NonCommutativeMultiply at x+y:
Use NonCommutativeExpand to expand the power of sum:
The third GeneralizedPower is equivalent to applying the operation to three copies of the argument:
Scope (5)
Power of a symbolic operation f:
Expand the power over an algebra with product f and vector space addition g:
GeneralizedPower of Plus and Times autosimplify:
Small positive integer GeneralizedPower of numeric functions evaluates at number arguments:
Powers of operations with built-in symbols:
Autosimplification of GeneralizedPower:
More general autosimplification for associative (Flat) operations:
Properties & Relations (2)
Text
Wolfram Research (2025), GeneralizedPower, Wolfram Language function, https://reference.wolfram.com/language/ref/GeneralizedPower.html.
CMS
Wolfram Language. 2025. "GeneralizedPower." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/GeneralizedPower.html.
APA
Wolfram Language. (2025). GeneralizedPower. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GeneralizedPower.html