GoodmanKruskalGammaTest

GoodmanKruskalGammaTest[v1,v2]

ベクトル v1 とベクトル v2 が独立かどうかの検定を行う．

GoodmanKruskalGammaTest[…,"property"]

"property"の値を返す．

詳細とオプション

  • GoodmanKruskalGammaTestは，ベクトルは独立であるという帰無仮説 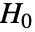とそうではないという対立仮説 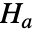で v1と v2に対して仮説検定を行う．
  • デフォルトで，確率の値すなわち 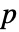値が返される．
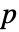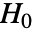  • 小さい 値は が真である可能性が低いことを示唆する．
  • 引数 v1と v2は長さが等しい任意の実ベクトルである．
  • GoodmanKruskalGammaTestは，GoodmanKruskalGamma[v1,v2]で計算されるGoodman–Kruskalガンマ係数 γ に基づいている．
  • GoodmanKruskalGammaTest[v1,v2,"HypothesisTestData"]はHypothesisTestDataオブジェクト htd を返す．このオブジェクトを使って htd["property"]の形で追加的な検定結果や特性を抽出することができる．
  • GoodmanKruskalGammaTest[v1,v2,"property"]を使って"property"の値を直接得ることができる．
  • 検定結果のレポートに関連する特性
  • "PValue"検定の 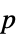値
    "PValueTable" 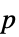値を含むフォーマットされた表
    "ShortTestConclusion"検定結果の短い記述
    "TestConclusion"検定結果の記述
    "TestData"検定統計量と 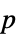値を含むリスト
    "TestDataTable"検定統計量と 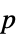値を含むフォーマットされた表
    "TestStatistic"検定統計量
    "TestStatisticTable"検定統計量を含むフォーマットされた表
  • 使用可能なオプション
  • AlternativeHypothesis "Unequal"対立仮説のための不等式
    Method Automatic 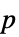値の計算に使用するメソッド
    SignificanceLevel 0.05診断とレポートのための切捨て
  • 独立性の検定のために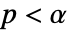， の場合にのみ 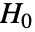が棄却されるような切捨て 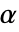が選ばれる．"TestConclusion"特性と"ShortTestConclusion" 特性に使われる 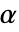の値はSignificanceLevelオプションで制御される．デフォルトで 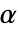は0.05に設定されている．

例題

すべて開くすべて閉じる

例  (1)

2つのベクトルが独立かどうかの検定を行う：

スコープ  (7)

検定  (4)

2つのベクトルが独立かどうかの検定を行う：

ベクトルが独立のとき， 値は一般に大きくなる：

従属関係があるときは， 値は一般に小さくなる：

特性を繰り返し取り出すためにHypothesisTestDataオブジェクトを作る：

抽出可能な特性：

HypothesisTestDataオブジェクトからいくつかの特性を抽出する：

検定からの 値と検定統計量：

任意数の特性を同時に抽出する：

検定からの 値と検定統計量：

レポート  (3)

検定結果を表にする：

検定結果の表：

レポートをカスタマイズするために検定の表から項目を取り出す：

値あるいは検定統計量を表にする：

表からの 値：

表からの検定統計量：

オプション  (7)

AlternativeHypothesis  (2)

デフォルトで両側検定が行われる：

両側検定を行うか，代りに片側検定を行うかする：

両側検定：

代りの2つの片側検定：

Method  (4)

デフォルトで，漸近的検定統計分布を使って 値が計算される：

値は置換法を使って得ることができる：

使用する置換回数を設定する：

デフォルトで，回の無作為置換が使われる：

無作為置換を生成するために使うシードを設定する：

SignificanceLevel  (1)

有意水準は"TestConclusion"と"ShortTestConclusion"に使われる：

特性と関係  (3)

ベクトル間の比較のために，検定統計量がGoodmanKruskalGammaとして計算される：

IndependenceTestを使って，適切な独立性の検定を選ぶことができる：

GoodmanKruskalGammaTestは使用できる検定の一つである：

GoodmanKruskalGammaTestは単調依存しか検知しない：

HoeffdingDTestを使うとより幅広い依存構造を検知することができる：

おもしろい例題  (1)

帰無仮説 が真のときの統計量を計算する：

特定の対立仮説による検定統計：

検定統計の分布を比較する：

Wolfram Research (2012), GoodmanKruskalGammaTest, Wolfram言語関数， https://reference.wolfram.com/language/ref/GoodmanKruskalGammaTest.html.

テキスト

Wolfram Research (2012), GoodmanKruskalGammaTest, Wolfram言語関数， https://reference.wolfram.com/language/ref/GoodmanKruskalGammaTest.html.

CMS

Wolfram Language. 2012. "GoodmanKruskalGammaTest." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/GoodmanKruskalGammaTest.html.

APA

Wolfram Language. (2012). GoodmanKruskalGammaTest. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GoodmanKruskalGammaTest.html

BibTeX

@misc{reference.wolfram_2024_goodmankruskalgammatest, author="Wolfram Research", title="{GoodmanKruskalGammaTest}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/GoodmanKruskalGammaTest.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_goodmankruskalgammatest, organization={Wolfram Research}, title={GoodmanKruskalGammaTest}, year={2012}, url={https://reference.wolfram.com/language/ref/GoodmanKruskalGammaTest.html}, note=[Accessed: 21-November-2024 ]}