GradientOrientationFilter

GradientOrientationFilter[data,r]

gives the local orientation parallel to the gradient of data, computed using discrete derivatives of a Gaussian of pixel radius r, returning values between and .

GradientOrientationFilter[data,{r,σ}]

uses a Gaussian with standard deviation σ.

Details and Options

  • GradientOrientationFilter is used to obtain the orientation of rapid-intensity change for applications such as texture and fingerprint analysis, as well as object detection and recognition.
  • The data can be any of the following:
  • listarbitrary-rank numerical array
    imagearbitrary Image or Image3D object
  • GradientOrientationFilter[data,r] uses standard deviation .
  • GradientOrientationFilter[data,…] returns the orientation as hyperspherical polar coordinate angles. For data arrays of dimensions , for , the resulting array will be of dimensions . The tuples in the resulting array denote the -spherical angles.
  • By default, defined angles are returned in the interval and the value is used for undefined orientation angles.
  • For a single channel image and for data, the gradient at a pixel position is approximated using discrete derivatives of Gaussians in each dimension.
  • For multichannel images, define the Jacobian matrix to be , where is the gradient for channel . The orientation is based on the direction of the eigenvector of that has the largest magnitude eigenvalue. This is the direction that maximizes the variation of pixel values.
  • For data arrays with dimensions, a coordinate system that corresponds to Part indices is assumed such that a coordinate {x1,…,xn} corresponds to data[[x1,…,xn]]. For images, the filter is effectively applied to ImageData[image].
  • In 1D, the orientation for nonzero gradients is always {0}, and undefined otherwise.
  • In 2D, the orientation is the angle such that is a unit vector parallel to .
  • In 3D, the orientation is represented by the angles such that is a unit vector parallel to the computed gradient.
  • For -dimensional data with , the orientation is given by angles such that is a unit vector in the direction of the computed gradient.
  • GradientOrientationFilter[image,…] always returns a single-channel image for 2D images and a two-channel image for 3D images. The result is of the same dimensions as image.
  • The following options can be specified:
  • Method Automaticconvolution kernel
    Padding "Fixed"padding method
    WorkingPrecision Automaticthe precision to use
  • The following suboptions can be given to Method:
  • "DerivativeKernel""Bessel"convolution kernel
    "UndefinedOrientationValue"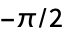-pi/2return value when orientation is undefined
  • Possible settings for "DerivativeKernel" include:
  • "Bessel"standardized Bessel derivative kernel, used for Canny edge detection
    "Gaussian"standardized Gaussian derivative kernel, used for Canny edge detection
    "ShenCastan"first-order derivatives of exponentials
    "Sobel"binomial generalizations of the Sobel edge-detection kernels
    {kernel1,kernel2,…}explicit kernels specified for each dimension
  • With a setting Padding->None, GradientOrientationFilter[data,…] normally gives an array or image smaller than data.

Examples

open allclose all

Basic Examples  (3)

Gradient orientation of a multichannel image:

Gradient orientation of a 3D image:

Gradient orientation filter of a 2D array:

Scope  (7)

Data  (5)

Gradient orientation of a vector:

Compute gradient orientation symbolically:

Gradient orientation of a binary image:

Gradient orientation of a grayscale image:

Gradient orientation of a diamond-shaped object:

Parameters  (2)

Gradient orientation filtering using increasing radii:

Gradient orientation filtering using different standard derivations:

Options  (8)

Padding  (3)

By default, a "Fixed" padding is used:

Specify a custom padding:

Padding->None normally returns an image smaller than the input image:

Method  (2)

By default, the "Bessel" kernel is used to compute the gradient derivatives:

Use the "ShenCastan" derivative kernel:

The difference between the two methods:

Specify the value for undefined orientation:

WorkingPrecision  (3)

MachinePrecision is by default used with integer arrays:

Perform exact computation instead:

With real arrays, the precision of the input is used by default:

WorkingPrecision is ignored when filtering images:

An image of a real type is always returned:

Applications  (5)

Identify the dominant orientations in a noisy image:

Compute and visualize the histogram distribution of weighted orientations:

Compute the histogram of oriented gradient (HOG) for an image, where each pixel casts a vote weighted by its gradient magnitude in the bin corresponding to its local orientation:

Visualize the gradient vectors of an image:

Express orientations in the standard image coordinate system:

Visualize the orientation of points on the boundary of the glyph:

Show the orientation of features in a fingerprint:

Properties & Relations  (2)

GradientOrientationFilter is invariant to the size of numbers in the data:

Gradient orientation filtering of an image gives a grayscale image of a real type:

Possible Issues  (1)

Gradient orientation filtering usually returns out-of-range pixel values:

Adjusting for brightness creates a more visible gradient orientation image:

Wolfram Research (2012), GradientOrientationFilter, Wolfram Language function, https://reference.wolfram.com/language/ref/GradientOrientationFilter.html (updated 2015).

Text

Wolfram Research (2012), GradientOrientationFilter, Wolfram Language function, https://reference.wolfram.com/language/ref/GradientOrientationFilter.html (updated 2015).

CMS

Wolfram Language. 2012. "GradientOrientationFilter." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/GradientOrientationFilter.html.

APA

Wolfram Language. (2012). GradientOrientationFilter. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GradientOrientationFilter.html

BibTeX

@misc{reference.wolfram_2024_gradientorientationfilter, author="Wolfram Research", title="{GradientOrientationFilter}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/GradientOrientationFilter.html}", note=[Accessed: 30-December-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_gradientorientationfilter, organization={Wolfram Research}, title={GradientOrientationFilter}, year={2015}, url={https://reference.wolfram.com/language/ref/GradientOrientationFilter.html}, note=[Accessed: 30-December-2024 ]}