GradientOrientationFilter

GradientOrientationFilter[data,r]

画素半径 r のガウス離散導関数を使って計算され，から までの値を返す，data の勾配に平行な局所方向を与える．

GradientOrientationFilter[data,{r,σ}]

標準偏差 σ でガウシアンを用いる．

詳細とオプション

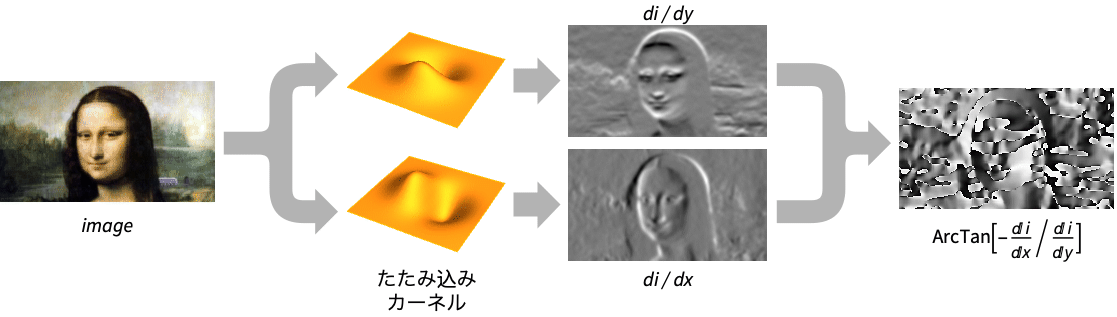
  • GradientOrientationFilterは，テクスチャおよび指紋の解析やオブジェクトの検知および認識のために，急速な強度変化の方向を求めるために使われる．
  • data は次のいずれでもよい．
  • list任意階数の数値配列
    image任意のImageオブジェクトまたはImage3Dオブジェクト
  • GradientOrientationFilter[data,r]は，標準偏差 を使う．
  • GradientOrientationFilter[data,…]は方向を超球極座標の角度として返す．次元 の配列については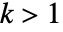，で，結果の配列の次元は になる．結果の配列の タプルは 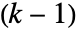球面角を表す．
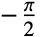  • デフォルトで，定義された角度が区間で返される．未定義の方位角には値が使われる．
  • 1チャンネル画像とデータの場合，画素位置の勾配 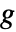は各次元についてガウス離散導関数を使って近似される．
  • 多チャンネル画像について，ヤコビ行列 がになるように定義する．ただし， はチャンネル 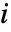の勾配である．方向は最大固有値を持つ 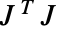の固有ベクトルの方向に基づいている．これが画素値の変化を最大にする方向である．
  • 次元の data 配列の場合は，Part指標に対応する座標系は，座標{x1,…,xn}が data[[x1,…,xn]]に対応するような座標系であるとみなされる．画像の場合は，事実上ImageData[image]にフィルタがかけられる．
  • 1Dでは，非零勾配の方向は常に{0}であり，その他の場合は定義されない．
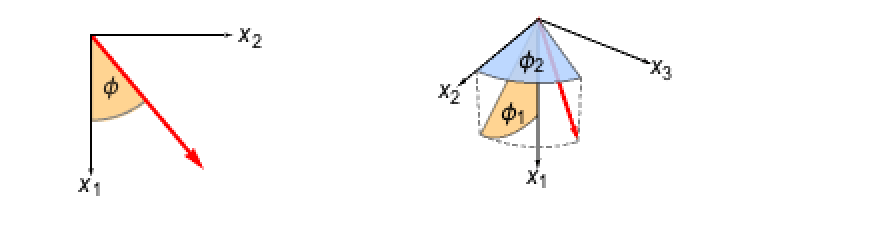
  • 2Dでは，方向は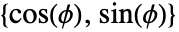が 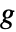に平行の単位ベクトルとなるような角度 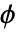である．
  • 3Dでは，勾配は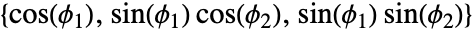が計算された勾配と平行な単位ベクトルとなるような角度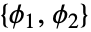で表される．
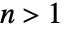  • である 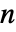次元データの場合，方向はが計算された勾配の方向での単位ベクトルであるような角度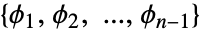で与えられる．
  • GradientOrientationFilter[image,…]は，2D画像に対しては単一チャンネルの画像を，3D画像に対しては2チャンネル画像を常に返す．結果は image と同じ次元である．
  • 指定可能なオプション
  • Method Automaticたたみ込みカーネル
    Padding "Fixed"充填方法
    WorkingPrecision Automatic使用精度
  • Methodには，次のサブオプションを与えることができる．
  • "DerivativeKernel""Bessel"たたみ込みカーネル
    "UndefinedOrientationValue"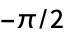-pi/2方向が決まっていないときに戻される値
  • "DerivativeKernel"の可能な設定
  • "Bessel"標準化されたベッセル(Bessel)導関数カーネル，Cannyエッジ検出に使われる
    "Gaussian"標準化されたガウス導関数カーネル．Cannyエッジ検出に使われる
    "ShenCastan"指数の一次導関数
    "Sobel"Sobelエッジ検出カーネルの二項一般化
    {kernel1,kernel2,…}各次元に指定される明示的なカーネル
  • Padding->Noneと設定すると，GradientOrientationFilter[data,…]は，通常は，data より小さい配列または画像を返す．

例題

すべて開くすべて閉じる

例  (3)

多チャンネル画像の勾配方向：

3D画像の勾配方向：

2D配列の勾配方向フィルタ：

スコープ  (7)

データ  (5)

ベクトルの勾配方向：

勾配方向を記号的に計算する：

バイナリ画像の勾配方向：

グレースケール画像の勾配方向：

ダイヤモンド型のオブジェクトの勾配方向：

Parameters  (2)

半径の増大を使った勾配方向フィルタリング：

異なる標準偏差を使った勾配方向フィルタリング：

オプション  (8)

Padding  (3)

デフォルトで，"Fixed"充填が使用される：

カスタム充填を指定する：

Padding->Noneは，通常は，入力画像より小さい画像を返す：

Method  (2)

デフォルトで，勾配微分は"Bessel"カーネルを使って計算される：

"ShenCastan"微分カーネルを使う：

2つのメソッドの差：

未定義の方向の値を指定する：

WorkingPrecision  (3)

MachinePrecisionは，デフォルトで，整数配列で使われる：

代りに厳密計算を行う：

実数配列では，デフォルトで入力精度が使われる：

画像にフィルタを適用する際は，WorkingPrecisionは無視される：

常に実数型の画像が返される：

アプリケーション  (5)

ノイズの多い画像の主な方向を特定する：

重み付きの方向のヒストグラム分布を計算し可視化する：

画像の勾配方向ヒストグラム(HOG)を計算する．各画素は局所方向に相当するビンの中の勾配の大きさで重みがついた票を投じるものとする：

画像の勾配ベクトルを可視化する：

標準的な画像座標系で方向を示す：

グリフの境界上の点の方向を可視化する：

指紋の特徴の方向を示す：

特性と関係  (2)

GradientOrientationFilterは，データ中の数の大きさに対して不変である：

画像に勾配方向フィルタリングを適用すると，実数型のグレースケール画像が返される：

考えられる問題  (1)

勾配方向フィルタは通常範囲外の画素値を返す：

明度で調整するとよりはっきりした勾配方向の画像ができる：

Wolfram Research (2012), GradientOrientationFilter, Wolfram言語関数， https://reference.wolfram.com/language/ref/GradientOrientationFilter.html （2015年に更新）.

テキスト

Wolfram Research (2012), GradientOrientationFilter, Wolfram言語関数， https://reference.wolfram.com/language/ref/GradientOrientationFilter.html （2015年に更新）.

CMS

Wolfram Language. 2012. "GradientOrientationFilter." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/GradientOrientationFilter.html.

APA

Wolfram Language. (2012). GradientOrientationFilter. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GradientOrientationFilter.html

BibTeX

@misc{reference.wolfram_2024_gradientorientationfilter, author="Wolfram Research", title="{GradientOrientationFilter}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/GradientOrientationFilter.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_gradientorientationfilter, organization={Wolfram Research}, title={GradientOrientationFilter}, year={2015}, url={https://reference.wolfram.com/language/ref/GradientOrientationFilter.html}, note=[Accessed: 21-November-2024 ]}