WOLFRAM

Wolfram言語 ＆ システムドキュメントセンター

GraphProduct[g1,g2]

グラフ g1とグラフ g2の直積を与える．

GraphProduct[g1,g2,"op"]

グラフ g1と g2についてタイプ"op"の積を与える．

詳細とオプション
Details and Options Details and Options
例題  
例  
スコープ  
有向グラフ  
無向グラフ  
混合グラフ  
多重グラフ  
重み付きグラフ  
特殊グラフ  
特性と関係  
関連項目
関連するガイド
履歴
引用書式

GraphProduct

GraphProduct[g1,g2]

グラフ g1とグラフ g2の直積を与える．

GraphProduct[g1,g2,"op"]

グラフ g1と g2についてタイプ"op"の積を与える．

詳細とオプション

  • GraphProductはボックス積としても知られている．
  • GraphProductは，通常，初期のグラフのブール結合から新たなグラフを生成するために使われる．
  • GraphProduct[g1,g2]は，g1と g2の頂点の直積から形成される頂点を持つグラフを与える．u1v1で u2が v2に接続されている，あるいは u2v2で u1が v1に接続されているなら，頂点{u1,u2}と{v1,v2}は接続されている．
  • GraphProduct[g1,g2,"op"]はタイプ"op"で辺{u1,u2}{v1,v2}が以下の条件に従うグラフ積を与える．
  • "Cartesian"(u1v1 ∧ u2v2)∨(u2v2∧u1v1)
    "Conormal"(u1v1)∨(u2v2)
    "Lexicographical"(u1v1)∨(u1v1∧u2v2)
    "Normal"(u1v1∧u2v2)∨(u2v2∧u1v1)∨(u1v1∧u2v2)
    "Rooted"(u1v1 ∧ u2v2)∨(u1v1 ∧ u2v2r)
    "Tensor"(u1v1)∧(u2v2)
  • 頂点 r はVertexList[g2]の最初の頂点である．
  • GraphProduct[g1,g2]は，事実上，GraphProduct[g1,g2,"Cartesian"]に等しい．
  • GraphProductは無向グラフ，有向グラフ，多重グラフ，混合グラフに使うことができる．

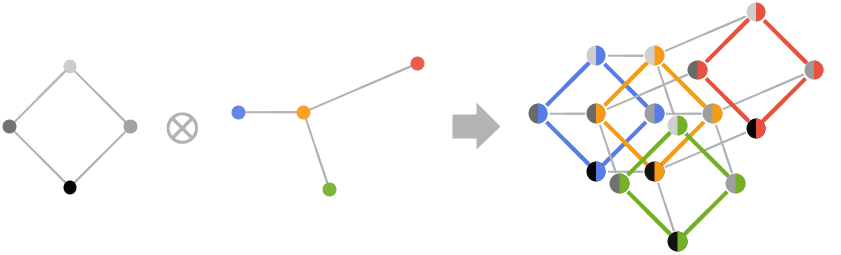
例題

すべて開く すべて閉じる

例  (3)

2つのグラフの直積を得る：

Wolfram Language code: GraphProduct[[image], [image]]

グラフ積の表：

Wolfram Language code: Table[GraphProduct[[image], [image], op, Rule[...]], {op, {...}}]

格子グラフを生成する：

Wolfram Language code: GraphProduct[PathGraph[{1, 2, 3}], PathGraph[{1, 2, 3, 4}], GraphLayout -> "GridEmbedding"]

トーラスグラフ：

Wolfram Language code: GraphProduct[CycleGraph[10], CycleGraph[6], GraphLayout -> "SpringElectricalEmbedding"]

スコープ  (30)

有向グラフ  (5)

GraphProductは有向グラフに使うことができる：

Wolfram Language code: GraphProduct[[image], [image]]

単純な有向グラフ：

Wolfram Language code: GraphProduct[[image], [image]]

多重有向グラフ：

Wolfram Language code: GraphProduct[[image], [image]]

重み付き有向グラフ：

Wolfram Language code: GraphProduct[[image], [image]]

注釈付き有向グラフ：

Wolfram Language code: GraphProduct[[image], [image]]

無向グラフ  (5)

GraphProductは無向グラフに使うことができる：

Wolfram Language code: GraphProduct[[image], [image]]

単純な無向グラフ：

Wolfram Language code: GraphProduct[[image], [image]]

多重無向グラフ：

Wolfram Language code: GraphProduct[[image], [image]]

重み付き無向グラフ：

Wolfram Language code: GraphProduct[[image], [image]]

注釈付き無向グラフ：

Wolfram Language code: GraphProduct[[image], [image]]

混合グラフ  (5)

GraphProductは混合グラフに使うことができる：

Wolfram Language code: GraphProduct[[image], [image]]

単純な混合グラフ：

Wolfram Language code: GraphProduct[[image], [image]]

多重混合グラフ：

Wolfram Language code: GraphProduct[[image], [image]]

重み付き混合グラフ：

Wolfram Language code: GraphProduct[[image], [image]]

注釈付き混合グラフ：

Wolfram Language code: GraphProduct[[image], [image]]

多重グラフ  (5)

GraphProductは多重グラフに使うことができる：

Wolfram Language code: GraphProduct[[image], [image]]

有向多重グラフ：

Wolfram Language code: GraphProduct[[image], [image]]

混合多重グラフ：

Wolfram Language code: GraphProduct[[image], [image]]

重み付き多重グラフ：

Wolfram Language code: GraphProduct[[image], [image]]

注釈付き多重グラフ：

Wolfram Language code: GraphProduct[[image], [image]]

重み付きグラフ  (5)

GraphProductは重み付きグラフに使うことができる：

Wolfram Language code: GraphProduct[[image], [image]]

重み付き有向グラフ：

Wolfram Language code: GraphProduct[[image], [image]]

重み付き無向グラフ：

Wolfram Language code: GraphProduct[[image], [image]]

重み付き混合グラフ：

Wolfram Language code: GraphProduct[[image], [image]]

注釈付き重み付きグラフ：

Wolfram Language code: GraphProduct[[image], [image]]

特殊グラフ  (5)

GraphProductは実体グラフに使うことができる：

Wolfram Language code: GraphProduct[["petersen graph"], ["petersen graph"]]

GraphProductは木に使うことができる：

Wolfram Language code: GraphProduct[[image], [image]]

規則を使ってグラフを指定する：

Wolfram Language code: GraphProduct[{1 -> 2, 2 -> 3, 3 -> 4, 4 -> 1}, {1 -> 2}]

GraphProductは3つ以上のグラフに使うことができる：

Wolfram Language code: GraphProduct[[image], [image], [image]]

異なるグラフの積のリストを生成する：

Wolfram Language code: {g, h} = {[image], [image]};
Wolfram Language code: Table[GraphProduct[g, h, type], {type, {"Cartesian", "Tensor", "Lexicographical", "Normal", "Conormal", "Rooted"}}]

特性と関係  (6)

頂点 viを持つ2つのグラフの積の頂点数は v1 v2 である：

Wolfram Language code: g = [image]; h = [image];
Wolfram Language code: VertexCount[GraphProduct[g, h]] == VertexCount[g] * VertexCount[h]

頂点 viと辺 eiを持つ2つの無向グラフのデカルト積の辺数はv1 e2+v2 e1である：

Wolfram Language code: g = [image]; h = [image];
Wolfram Language code: {v1, v2} = VertexCount /@ {g, h};
Wolfram Language code: {e1, e2} = EdgeCount /@ {g, h};
Wolfram Language code: EdgeCount@GraphProduct[g, h, "Cartesian"] == v1 * e2 + v2 * e1

テンソル積は2 e1e2である：

Wolfram Language code: EdgeCount@GraphProduct[g, h, "Tensor"] == 2e1 e2

辞書式順序の積はv1 e2+ e1v22 である：

Wolfram Language code: EdgeCount@GraphProduct[g, h, "Lexicographical"] == v1 * e2 + e1 * v2 ^ 2

法線の積はv1 e2+v2 e1 + 2 e1e2である：

Wolfram Language code: EdgeCount@GraphProduct[g, h, "Normal"] == v1 * e2 + v2 * e1 + 2e1 e2

共法線積はv12 e2+ e1v22 - 2e1e2である：

Wolfram Language code: EdgeCount@GraphProduct[g, h, "Conormal"] == v1 ^ 2 * e2 + e1 * v2 ^ 2 - 2e1 e2

根付き積はv1 e2+ e1である：

Wolfram Language code: EdgeCount@GraphProduct[g, h, "Rooted"] == v1 * e2 + e1

2つの単一辺の直積は巡回である：

Wolfram Language code: GraphProduct[[image], [image], "Cartesian"]

2つの単一辺の法線積は完全グラフである：

Wolfram Language code: GraphProduct[[image], [image], "Normal"]

2つの単一辺のテンソル積はクロスである：

Wolfram Language code: GraphProduct[[image], [image], "Tensor"]

TorusGraph[{m,n}]は巡回グラフ と の直積から形成されるグラフである：

Wolfram Language code: g = TorusGraph[{10, 6}]
Wolfram Language code: h = GraphProduct[CycleGraph[10], CycleGraph[6]]
Wolfram Language code: IsomorphicGraphQ[g, h]
Wolfram Research (2022), GraphProduct, Wolfram言語関数， https://reference.wolfram.com/language/ref/GraphProduct.html.

テキスト

Wolfram Research (2022), GraphProduct, Wolfram言語関数， https://reference.wolfram.com/language/ref/GraphProduct.html.

CMS

Wolfram Language. 2022. "GraphProduct." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/GraphProduct.html.

APA

Wolfram Language. (2022). GraphProduct. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GraphProduct.html

BibTeX

@misc{reference.wolfram_2026_graphproduct, author="Wolfram Research", title="{GraphProduct}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/GraphProduct.html}", note=[Accessed: 22-August-2026]}

BibLaTeX

@online{reference.wolfram_2026_graphproduct, organization={Wolfram Research}, title={GraphProduct}, year={2022}, url={https://reference.wolfram.com/language/ref/GraphProduct.html}, note=[Accessed: 22-August-2026]}