GraphUnion

GraphUnion[g1,g2]

gives the graph union of the graphs g1 and g2.

GraphUnion[g1,g2,…]

gives the graph union of g1, g2, ….

GraphUnion[{vw,…},…]

uses rules vw to specify the graph g.

Details and Options

  • The graph union Graph[v1,e1]⋃Graph[v2,e2] is given by Graph[v1⋃v2,e1⋃e2].
  • GraphUnion works with undirected graphs, directed graphs, multigraphs, and mixed graphs.

Background & Context

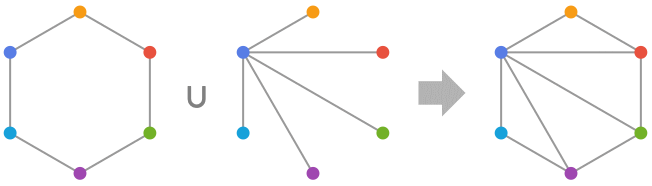
  • GraphUnion gives a new graph obtained from a set of two or more directed or undirected graphs obtained by separately taking the union of the original vertex and edge sets. For edges with the same vertex labels in different graphs, GraphUnion keeps only one of them. The resulting graph keeps the vertex labels of the unique original edges.
  • Related functions include GraphDisjointUnion, GraphIntersection, and GraphDifference. Unlike GraphUnion, GraphDisjointUnion keeps all edges even if multiple edges exist in different graphs that have the same vertex labels. GraphIntersection gives the graph obtained from the union of vertex sets and intersection of edge sets of the original graphs. GraphDifference gives the graph obtained from the union of vertex sets of two graphs and the complement of the second graph’s edge set with respect to the first. GraphComplement gives the graph that has the same vertex set as a given graph, but with edges corresponding to absent edges in the original (and vice versa).

Examples

open allclose all

Basic Examples  (1)

Obtain the graph union of two graphs:

Highlight the graph union:

Scope  (6)

GraphUnion works with undirected graphs:

Directed graphs:

Multigraphs:

Mixed graphs:

Use rules to specify the graph:

GraphUnion works with more than two graphs:

Properties & Relations  (7)

The vertices of the graph union are the union of the vertices of the graphs:

The edges of the graph union are the union of the edges of the graphs:

The graph union of a graph and its subgraph is isomorphic to itself:

The graph union of any simple graph and its complement is a complete graph:

The GraphUnion of two graphs has the same vertices as GraphDifference:

The GraphUnion of two graphs has the same vertices as GraphIntersection:

The GraphDisjointUnion can be found using GraphUnion:

Wolfram Research (2010), GraphUnion, Wolfram Language function, https://reference.wolfram.com/language/ref/GraphUnion.html (updated 2015).

Text

Wolfram Research (2010), GraphUnion, Wolfram Language function, https://reference.wolfram.com/language/ref/GraphUnion.html (updated 2015).

CMS

Wolfram Language. 2010. "GraphUnion." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/GraphUnion.html.

APA

Wolfram Language. (2010). GraphUnion. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GraphUnion.html

BibTeX

@misc{reference.wolfram_2024_graphunion, author="Wolfram Research", title="{GraphUnion}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/GraphUnion.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_graphunion, organization={Wolfram Research}, title={GraphUnion}, year={2015}, url={https://reference.wolfram.com/language/ref/GraphUnion.html}, note=[Accessed: 21-November-2024 ]}