Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how

Wolfram Language & System Documentation Center

HermiteReduce

HermiteReduce

HermiteReduce[m]

gives the Hermite normal form of an integer matrix .

Details

The result is an upper triangular matrix. It is obtained from the input matrix by a unimodular matrix factor.
An integer matrix is unimodular if it has determinant of 1 or 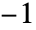. This means it can be inverted over the integers, that is, without requiring fractions.
HermiteReduce is similar to RowReduce, except that divisions are not allowed. In effect, the GCD operation replaces division. Pivots need not be one, and similarly, elements above such pivots need not be zero.

Examples

open all close all

Basic Examples (1)

Compute the Hermite reduction of a matrix:

Scope (12)

Basic Uses (8)

Find the Hermite reduction of an integer square matrix:

Hermite reduction of a singular matrix:

The number of nonzero rows in r is equal to the rank of m:

Hermite reduction for a rectangular matrix:

Use HermiteReduce for a rational matrix:

Hermite reduction for a Gaussian integer matrix:

Hermite reduction for a Gaussian rational matrix:

Hermite decomposition does not work with inexact numbers:

The Hermite decomposition for a large, integer matrix is computed efficiently:

Special Matrices (4)

Find the Hermite reduction for sparse matrices:

Hermite reductions of structured matrices:

Hermite reduction of an IdentityMatrix is simply an identity matrix:

Hermite reduction of HilbertMatrix:

Applications (3)

HermiteReduce can be used to determine if two integer lattices are equivalent. If the generators of the lattices are put in row matrices, the lattices are equal if and only if the Hermite reductions of the corresponding matrices are the same. Consider the lattices generated by , , and , , :

As the reduced matrices of and are equal, the two sets of generators create the same lattice:

Confirm the result using LatticeReduce, which gives the same reduction up to overall sign:

Solve a linear Diophantine equation :

Form a homogenized system:

Rows of are integer combinations of rows of :

The second row of gives a solution of :

The last two rows of give a basis of solutions to the homogeneous equation :

The Smith reduction can often be found by two iterations of the Hermite reduction:

A second application, to $TemplateBox[{{(, {r, _, 1}, )}}, Transpose]$ , gives a diagonal matrix:

Compare with the result given by SmithReduce:

Properties & Relations (7)

HermiteReduce gives the second matrix output by HermiteDecomposition:

HermiteReduce gives an upper triangular matrix:

For an matrix , HermiteReduce[a] has the same dimensions:

The Hermite reduction matrix has integer values if the input matrix is integer:

If the input matrix has noninteger rational elements, so will the result:

For a rational input, the entries of the reduced matrix are non-negative:

For complex-valued input, the imaginary parts of the entries are non-negative:

The real parts can be negative:

Elements of form an upper triangular basis of the lattice generated by the rows of m:

LatticeReduce gives a basis consisting of shorter vectors:

HermiteReduce works over the Euclidean ring of the integers:

The entries above each pivot are always smaller in absolute value than that pivot:

In contrast, PolynomialHermiteReduce works over the Euclidean ring of univariate polynomials:

Now the entries above each pivot are always lower in degree than that pivot:

Note that integers and polynomials are different as rings, and in particular one does not recover anything resembling the integer Hermite form by making the polynomial variable zero:

Top