HeunG
HeunG[a,q,α,β,γ,δ,z]
一般Heun関数を与える.
詳細

- HeunGは関数のHeun族に属し,直接Hypergeometric2F1関数を一般化し,量子力学,数学物理およびそのアプリケーションでしばしば使われる.
- 記号操作・数値操作の両方に適した数学関数である.
- HeunG[a,q,α,β,γ,δ,z]は一般Heun微分方程式
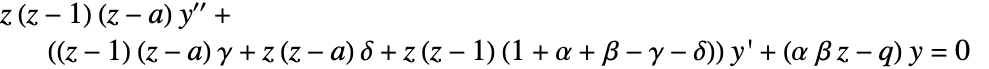 を満足する.
を満足する. - HeunG関数は,制約条件HeunG[a,q,α,β,γ,δ,0]=1を満足する一般Heun方程式の正則解である.
- HeunGは,
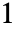 から
から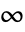 までおよび
までおよび 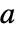 からDirectedInfinity[a]までの複素
からDirectedInfinity[a]までの複素 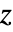 平面上に1本の不連続な分枝切断線を持つ.
平面上に1本の不連続な分枝切断線を持つ. - HeunGは,特定の特殊な引数については自動的に厳密値に評価される.
- HeunGは任意の複素パラメータについて評価できる.
- HeunGは任意の数値精度で評価できる.
- HeunGは自動的にリストに縫い込まれる.
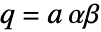 かつ
かつ 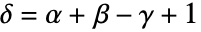 または
または 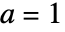 かつ
かつ 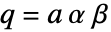 であれば,HeunG[a,q,α,β,γ,δ,z]はHypergeometric2F1[α,β,γ,z]に特化される.
であれば,HeunG[a,q,α,β,γ,δ,z]はHypergeometric2F1[α,β,γ,z]に特化される.
例題
すべて開くすべて閉じるスコープ (37)
数値評価 (10)
HeunGは1つあるいは複数の複素パラメータを取ることができる:
HeunGは複素引数を取ることができる:
さらに,HeunGはすべての複素入力を取ることができる:
HeunGを高精度で効率よく評価する:
![]() から
から![]() までの分枝切断線における点についてHeunGを評価する:
までの分枝切断線における点についてHeunGを評価する:
![]() から DirectedInfinity[a]までの分枝切断線上の点についてHeunGを評価する:
から DirectedInfinity[a]までの分枝切断線上の点についてHeunGを評価する:
MatrixFunctionを使って行列のHeunG関数を計算することもできる:
特定の値 (8)
原点におけるHeunGの値:
確定特異点 ![]() におけるHeunGの値は不定である:
におけるHeunGの値は不定である:
確定特異点 ![]() におけるHeunGの値は不定である:
におけるHeunGの値は不定である:
「対数」の場合,すなわち非正整数 ![]() についてのHeunGの値は定まらない:
についてのHeunGの値は定まらない:
![]() ならばHeunGの値は定まらない:
ならばHeunGの値は定まらない:
![]() かつ
かつ ![]() であれば,HeunGは自動的にHypergeometric2F1関数に評価される:
であれば,HeunGは自動的にHypergeometric2F1関数に評価される:
![]() かつ
かつ ![]() であれば,HeunGを評価すると自動的にHypergeometric2F1関数になる:
であれば,HeunGを評価すると自動的にHypergeometric2F1関数になる:
ある特定のパラメータについては,HeunGを評価すると自動的により簡単な関数になる:
可視化 (5)
関数の特性 (3)
Hypergeometric2F1はHeunGの特殊ケースである:
HeunGは,非線形引数のときには,簡約されてHypergeometric2F1関数になることがある:
HeunGは,特殊ケースでは,簡約された有理関数になることがある:
微分 (4)
HeunGの ![]() 次導関数はHeunGPrimeである:
次導関数はHeunGPrimeである:
HeunGのより高次の導関数はHeunGPrimeを使って計算される:
特殊なケースのパラメータについてのHeunGの導関数:
特殊なケースのパラメータを含むHeunGのより高次の導関数:
アプリケーション (5)
特性と関係 (6)
HeunGは原点において解析的である:
![]() および
および ![]() はHeunG関数の特異点である:
はHeunG関数の特異点である:
HeunGは,これら2つの特異点を除いては任意の有限複素 ![]() において計算できる:
において計算できる:
HeunGの導関数はHeunGPrimeである:
HeunGはパラメータ ![]() と
と ![]() の間で対称ある:
の間で対称ある:
引数 ![]() と特異点
と特異点 ![]() を不変のままにする,パラメータ変換に対応するHeunGについての等価な4つの式:
を不変のままにする,パラメータ変換に対応するHeunGについての等価な4つの式:
Seriesを使って ![]() における最後の式の級数展開が最初のもののそれと一致することを示す:
における最後の式の級数展開が最初のもののそれと一致することを示す:
パラメータ ![]() と
と ![]() を不変のままにする,引数変換に対応するHeunGについての6つの同等の式:
を不変のままにする,引数変換に対応するHeunGについての6つの同等の式:
Seriesを使って ![]() における最後の5つの式の級数展開がt最初のもののそれと一致することを示す:
における最後の5つの式の級数展開がt最初のもののそれと一致することを示す:
おもしろい例題 (1)
HeunGのいくつかの特殊ケースの表を作る:
テキスト
Wolfram Research (2020), HeunG, Wolfram言語関数, https://reference.wolfram.com/language/ref/HeunG.html.
CMS
Wolfram Language. 2020. "HeunG." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/HeunG.html.
APA
Wolfram Language. (2020). HeunG. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HeunG.html