HeunT
HeunT[q,α,γ,δ,ϵ,z]
gives the tri-confluent Heun function.
Details

- HeunT belongs to the Heun class of functions and occurs in quantum mechanics and applications.
- Mathematical function, suitable for both symbolic and numerical manipulation.
- HeunT[q,α,γ,δ,ϵ,z] satisfies the tri-confluent Heun differential equation
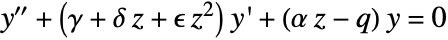 .
. - The HeunT function is the power-series solution
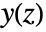 of the tri-confluent Heun equation that satisfies the conditions
of the tri-confluent Heun equation that satisfies the conditions 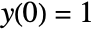 and
and 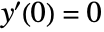 .
. - For certain special arguments, HeunT automatically evaluates to exact values.
- HeunT can be evaluated for arbitrary complex parameters.
- HeunT can be evaluated to arbitrary numerical precision.
- HeunT automatically threads over lists.
Examples
open allclose allScope (24)
Numerical Evaluation (8)
The precision of the output tracks the precision of the input:
HeunT can take one or more complex number parameters:
HeunT can take complex number arguments:
Finally, HeunT can take all complex number input:
Evaluate HeunT efficiently at high precision:
Compute the elementwise values of an array:
Or compute the matrix HeunT function using MatrixFunction:
Visualization (5)
Differentiation (2)
First ![]() -derivative of HeunT is HeunTPrime:
-derivative of HeunT is HeunTPrime:
Higher derivatives of HeunT are calculated using HeunTPrime:
Integration (3)
Applications (5)
Solve the tri-confluent Heun differential equation using DSolve:
Solve the initial value problem for the tri-confluent Heun differential equation:
Plot the solution for different values of the accessory parameter q:
Directly solve the tri-confluent Heun differential equation:
The quartic potential for the 1D Schrödinger equation:
Solve this general potential in terms of HeunT functions:
When ![]() , HeunT can be expressed in terms of Airy functions:
, HeunT can be expressed in terms of Airy functions:
Properties & Relations (4)
HeunT is analytic at the origin:
HeunT can be calculated at any finite complex ![]() :
:
The derivative of HeunT is HeunTPrime:
Use FunctionExpand to expand HeunT into simpler functions:
Possible Issues (1)
HeunT calculations might take time for big arguments:
Neat Examples (1)
The classical anharmonic oscillator equation is solved in terms of HeunT:
Text
Wolfram Research (2020), HeunT, Wolfram Language function, https://reference.wolfram.com/language/ref/HeunT.html.
CMS
Wolfram Language. 2020. "HeunT." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/HeunT.html.
APA
Wolfram Language. (2020). HeunT. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/HeunT.html