Hexahedron[{p1,p2,…,p8}]
represents a filled hexahedron with corners p1, p2, …, p8.
Hexahedron[{{p1,1,p1,2,…,p1,8},{p2,1,…},…}]
represents a collection of hexahedra.


Hexahedron
Hexahedron[{p1,p2,…,p8}]
represents a filled hexahedron with corners p1, p2, …, p8.
Hexahedron[{{p1,1,p1,2,…,p1,8},{p2,1,…},…}]
represents a collection of hexahedra.
Details and Options

- Hexahedron can be used as a geometric region and a graphics primitive.
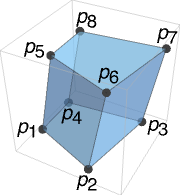
- Hexahedron represents a filled polyhedron given by the polygon faces {p4,p3,p2,p1}, {p1,p2,p6,p5}, {p2,p3,p7,p6}, {p3,p4,p8,p7}, {p4,p1,p5,p8}, and {p5,p6,p7,p8}.
- CanonicalizePolyhedron can be used to convert a hexahedron to an explicit Polyhedron object.
- Hexahedron can be used in Graphics3D.
- In graphics, the points pi can be Scaled and Dynamic expressions.
- Graphics rendering is affected by directives such as FaceForm, EdgeForm, Opacity, Texture, and color.
- The following options and settings can be used in graphics:
-
VertexColors Automatic vertex colors to be interpolated VertexNormals Automatic effective vertex normals for shading VertexTextureCoordinates None coordinates for textures
Examples
open all close allScope (18)
Graphics (8)
Styling (3)
FaceForm and EdgeForm can be used to specify the styles of the faces and edges:
Apply a Texture to the faces:
Assign VertexColors to vertices:
Coordinates (3)
Specify coordinates by fractions of the plot range:
Specify scaled offsets from the ordinary coordinates:
Points can be Dynamic:
Regions (10)
Embedding dimension is the dimension of the space in which the hexahedron lives:
Geometric dimension is the dimension of the shape itself:
Get conditions for point membership:
The equidistance contours for a hexahedron:
Nearest points to an enclosing sphere:
Integrate over a hexahedron region:
Applications (4)
Convert a Cuboid to a Hexahedron:
Convert a Parallelepiped to a Hexahedron:
Create a square frustum parameterized by base width, top width, and height:
Properties & Relations (4)
Hexahedron is a generalization of a Cuboid in dimension 3:
A hexahedron can be represented as the union of five tetrahedra:
Point index list of tetrahedra vertices:
A hexahedron can also be represented as the union of six tetrahedra:
ImplicitRegion can represent any Hexahedron:
Related Guides
Text
Wolfram Research (2014), Hexahedron, Wolfram Language function, https://reference.wolfram.com/language/ref/Hexahedron.html (updated 2019).
CMS
Wolfram Language. 2014. "Hexahedron." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/Hexahedron.html.
APA
Wolfram Language. (2014). Hexahedron. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Hexahedron.html
BibTeX
@misc{reference.wolfram_2025_hexahedron, author="Wolfram Research", title="{Hexahedron}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/Hexahedron.html}", note=[Accessed: 07-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_hexahedron, organization={Wolfram Research}, title={Hexahedron}, year={2019}, url={https://reference.wolfram.com/language/ref/Hexahedron.html}, note=[Accessed: 07-February-2026]}