ImagePeriodogram[image]
shows the squared magnitude of the discrete Fourier transform (power spectrum) of image.
ImagePeriodogram[image,n]
shows the average of power spectra of non-overlapping partitions of size n×n.
ImagePeriodogram[image,n,d]
uses partitions with offset d.
ImagePeriodogram[image,n,d,wfun]
applies a smoothing window wfun to each partition.
ImagePeriodogram[image,n,d,wfun,m]
pads partitions with zeros to length m prior to the computation of the transform.


ImagePeriodogram
ImagePeriodogram[image]
shows the squared magnitude of the discrete Fourier transform (power spectrum) of image.
ImagePeriodogram[image,n]
shows the average of power spectra of non-overlapping partitions of size n×n.
ImagePeriodogram[image,n,d]
uses partitions with offset d.
ImagePeriodogram[image,n,d,wfun]
applies a smoothing window wfun to each partition.
ImagePeriodogram[image,n,d,wfun,m]
pads partitions with zeros to length m prior to the computation of the transform.
Details and Options

- ImagePeriodogram logarithmically scales the power spectrum of the image and adjusts the values so that they range from 0 to 1.
- In ImagePeriodogram[image,n,d,wfun], the smoothing window wfun can be specified using a window function that will be sampled between
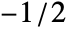 and
and 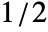 , or a list of length n. The default window is DirichletWindow, which effectively does no smoothing.
, or a list of length n. The default window is DirichletWindow, which effectively does no smoothing. - ImagePeriodogram[image,n] is equivalent to ImagePeriodogram[image,n,n,DirichletWindow,n].
- ImagePeriodogram[image,{n1,n2}] partitions image into blocks of size n1×n2.
- For 3D images, ImagePeriodogram[image,{n1,n2,n3}] partitions image into blocks of size n1×n2×n3.
- For multichannel images, ImagePeriodogram returns a multichannel image where each channel is the power spectrum computed for each channel separately.
- ImagePeriodogram accepts the Alignment option that determines the location of the zero frequency term. The default is Alignment->Center. With Alignment->{Left,Top}, the zero frequency term is placed at the top-left corner of the image.
Examples
open all close allOptions (1)
Properties & Relations (2)
Create the image periodogram from the power spectrum data:
Use PeriodogramArray to change the default visualization settings of the image power spectrum:
Related Guides
History
Text
Wolfram Research (2012), ImagePeriodogram, Wolfram Language function, https://reference.wolfram.com/language/ref/ImagePeriodogram.html.
CMS
Wolfram Language. 2012. "ImagePeriodogram." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ImagePeriodogram.html.
APA
Wolfram Language. (2012). ImagePeriodogram. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ImagePeriodogram.html
BibTeX
@misc{reference.wolfram_2025_imageperiodogram, author="Wolfram Research", title="{ImagePeriodogram}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/ImagePeriodogram.html}", note=[Accessed: 19-February-2026]}
BibLaTeX
@online{reference.wolfram_2025_imageperiodogram, organization={Wolfram Research}, title={ImagePeriodogram}, year={2012}, url={https://reference.wolfram.com/language/ref/ImagePeriodogram.html}, note=[Accessed: 19-February-2026]}