ImprovementImportance

ImprovementImportance[rdist,t]

ReliabilityDistribution rdist の時間 t におけるすべての成分の改善重要度を与える．

ImprovementImportance[fdist,t]

FailureDistribution fdist の時間 t におけるすべての成分の改善重要度を与える．

詳細

  • ImprovementImportanceは改善可能性としても知られる．
  • 成分 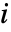の改善重要度は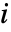， を完全な成分で置き換えたのであれば，SurvivalFunctionの増加である．
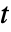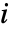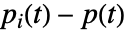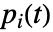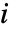  • 時間 における成分 の改善重要度は で与えられる．ただし，は 番目の成分が絶対に故障しない場合に系が動いている確率であり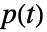，は系が動いている確率である．
  • 重要度の結果は rdist における分布リストで与えられる成分順で返される．

例題

すべて開くすべて閉じる

例  (3)

寿命分布が異なる，直列に繋がれた2つの成分：

結果はReliabilityDistributionにおける分布リストと同じ順序で与えられる：

寿命分布が異なる，並列に繋がれた2つの成分：

故障の木に基づくモデリングを使って系を定義する：

スコープ  (17)

ReliabilityDistributionモデル  (9)

等しい寿命分布を持ち並列接続された2つの成分：

両成分の改善可能性は等しい：

等しい寿命分布を持ち直列接続された2つの成分：

両成分の改善可能性は等しい：

寿命分布が等しい3つの成分のうち2つが動かなければならない系：

両成分の改善可能性は等しい：

寿命分布が等しい単純な混合形：

重要度を計算する：

成分 x を完全な成分で置き換えるのが最良である：

ある成分と並列に繋がれている直列接続の系：

重要度を計算する：

成分 を完全な成分で置き換えるのが最良である：

単純な混合系でパラメータを変更することの効果を調べる：

重要度を計算する：

並列成分の1つである を悪化させることによる重要度の変化を示す：

分布が異なる2つの他の成分と並列の1つの成分：

時間のある1点での重要性尺度を厳密な結果として求める：

機械精度による結果：

記号式による結果：

任意の有効なReliabilityDistributionを使うことができる：

あまり信頼性がない成分 を完全な成分で置き換えるのが信頼性にとってよりよい：

部分系の重要性尺度を得るために段階を追って系をモデル化する：

部分系はすでにより信頼性が高いので，重要度の改善可能性は低い：

FailureDistributionモデル  (8)

2つの基本事象のどちらも頂上事象に繋がる：

両成分の改善可能性は等しい：

両方の基本事象が一緒になってはじめて頂上事象に至る：

両成分の改善可能性は等しい：

基本事象の分布が等しいボーティングゲート：

ボーティングゲートにおける同一事象の改善可能性は等しい：

AndゲートとOrゲートの両方がある単純な系：

改善重要度を計算する：

事象 x の改善可能性が最も高い：

AndゲートとOrゲートの両方がある単純な系：

重要度を示す：

事象 x の改善可能性が最も高い：

単純な混合系におけるパラメータの変更の効果を調べる：

重要度を計算する：

基本事象の1つである z を悪化させた場合の重要度の変化を示す：

任意の有効なFailureDistributionを使うことができる：

重要性尺度をプロットする：

部分系の重要性尺度を得るために段階を追って系をモデル化する：

時間に沿って重要度をプロットする：

アプリケーション  (3)

3時間持続しなければならない系でどの成分を改善するのが最もよいかを求める：

改善重要度によると，成分 v を改善するのが最もよい：

1つの成分が直列で2つの成分が並列の系について調べる．改善重要度の尺度を使って，どの成分の重要度が最も高いかを見る：

成分 x と y の重要度が最も高い：

航空機の離陸時の信頼性を改善する可能性が最も高いのはどの成分かの分析を行う．格納扉は電動・手動のどちらで開けることもできる：

2つの燃料ポンプを動かすためには動力が必要である：

さらに2つのポンプを信頼できる電池を使って動かすことができる．したがって次の燃料移送構造となる：

航空機の除氷装置と燃料の収蔵タンクも必要である：

寿命分布を定義する：

重要度を計算する：

ポンプの改良が航空機の信頼性を改善する最大の可能性を持つ：

特性と関係  (3)

ImprovementImportanceはProbabilityで定義することができる：

成分を完全な成分で置き換えた場合の系の信頼性：

基盤の系の信頼性の違いを計算する：

定義と比較する：

ImprovementImportanceはBirnbaumImportanceで定義することができる：

すべての成分についてBirnbaumImportanceを計算する：

成分の信頼性のなさを掛ける：

定義と比較する：

無関係な成分の重要度は0である：

Wolfram Research (2012), ImprovementImportance, Wolfram言語関数， https://reference.wolfram.com/language/ref/ImprovementImportance.html.

テキスト

Wolfram Research (2012), ImprovementImportance, Wolfram言語関数， https://reference.wolfram.com/language/ref/ImprovementImportance.html.

CMS

Wolfram Language. 2012. "ImprovementImportance." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/ImprovementImportance.html.

APA

Wolfram Language. (2012). ImprovementImportance. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ImprovementImportance.html

BibTeX

@misc{reference.wolfram_2024_improvementimportance, author="Wolfram Research", title="{ImprovementImportance}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/ImprovementImportance.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_improvementimportance, organization={Wolfram Research}, title={ImprovementImportance}, year={2012}, url={https://reference.wolfram.com/language/ref/ImprovementImportance.html}, note=[Accessed: 21-November-2024 ]}