ImprovementImportance

ImprovementImportance[rdist,t]

给出所有元件在时间 t 的 ReliabilityDistribution rdist 中的改进重要度.

ImprovementImportance[fdist,t]

给出所有元件在时间 t 的 FailureDistribution fdist 中的改进重要度.

更多信息

  • ImprovementImportance 也称为改进潜力（improvement potential）.
  • 元件 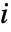的改进重要度是 SurvivalFunction 的增加量，如果 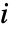用一个完美元件替换的话.
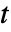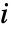  • 在时间 对元件 的改进重要度由 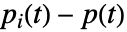给出，其中 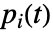是给定第 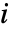个元件永远不失效的情况下，系统运作的概率，而 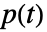是系统正在运作的概率.
  • 重要度结果以 rdist 中分布列表给出的元件顺序返回.

范例

打开所有单元关闭所有单元

基本范例  (3)

在不同寿命分布下，串行连接的两个元件：

结果以和 ReliabilityDistribution 中分布列表相同的顺序给出：

在不同寿命分布下，并行连接的两个元件：

使用基于树的故障模型定义系统：

范围  (17)

ReliabilityDistribution 模型  (9)

在相同寿命分布下，并行连接的两个元件：

两个元件对改进而言有相同的潜力（potential）：

在相同的寿命分布下，串行连接的两个元件：

对于改进而言，两个元件有相同的潜力（potential）：

在相同的寿命分布下，三个元件中有两个必须运作的系统：

两个元件对改进而言有相同的潜力（potential）：

在相同的寿命分布下的简单混合系统：

计算重要度：

元件 x 最好使用完美元件替换：

串联系统与一个元件并行连接：

计算重要度：

元件 最好使用完美元件替换：

研究参数改变对简单混合系统的影响：

计算重要度：

当使一个并联元件 变坏时，显示重要度的改变：

一个元件与其他两个服从不同分布的元件并联：

求时间中特定点的重要度测量，以精确结果表示：

作为机器精度的结果：

作为符号式表达式：

可以使用任意有效的 ReliabilityDistribution：

对于可靠性而言，最好将具有较低可靠性的元件 用完美元件替换：

对系统按步骤建模，以获取子系统的重要度测量：

子系统对于改进而言有较少的潜力（potential），因为它已经是更可靠的了：

FailureDistribution 模型  (8)

两个基本事件的任何一个会导致顶事件（top event）：

两个元件对改进而言有相同的潜力：

只有两个基本事件一起会导致顶事件：

对于改进而言，两个元件具有相同的潜力：

在基本事件下，具有相同分布的投票门（voting gate）：

对于改进而言，投票门中的相同事件具有相同的潜力（potential）：

具有 And 和 Or 门的简单系统：

计算改进重要度：

对于改进而言，事件 x 具有最高的潜力：

具有 And 和 Or 门的简单系统：

显示重要度：

事件 x 具有最高的改进潜力：

研究参数改变对简单混合系统的影响：

计算重要度：

当使一个基本事件 z 变差时，显示重要度的改变：

可以使用任意有效的 FailureDistribution：

绘制重要度测量图线：

按步骤对系统建模，以获取子系统的重要度测量：

绘制重要度随着时间变化的图线：

应用  (3)

求哪个元件对于改进已经运作了三个小时的系统最好：

根据改进重要度，元件 v 对改进最好：

研究具有一个串联元件和两个并联元件的系统. 判断根据改进重要度测量，哪个元件最重要：

元件 x 和 y 是最重要的元件：

分析对于改进飞行器发射可靠性而言，哪个元件具有最高的潜力. 飞机库的门可以通过电子或者手工方式打开：

两个燃油泵需要电力来运行：

运行在可靠的电池上的另外两个泵，提供以下的燃料转换结构：

还需要飞行器除冰器和燃料储存罐：

定义寿命分布：

计算重要度：

改进最可能提高可靠性的泵：

属性和关系  (3)

ImprovementImportance 可以使用 Probability 定义：

当元件使用一个完美元件替换时的系统可靠性：

计算与基本系统可靠性的差值：

与定义比较：

ImprovementImportance 可以使用 BirnbaumImportance 定义：

计算所有元件的 BirnbaumImportance：

乘以元件的不可靠度：

与定义比较：

无关元件的重要度为 0：

Wolfram Research (2012)，ImprovementImportance，Wolfram 语言函数，https://reference.wolfram.com/language/ref/ImprovementImportance.html.

文本

Wolfram Research (2012)，ImprovementImportance，Wolfram 语言函数，https://reference.wolfram.com/language/ref/ImprovementImportance.html.

CMS

Wolfram 语言. 2012. "ImprovementImportance." Wolfram 语言与系统参考资料中心. Wolfram Research. https://reference.wolfram.com/language/ref/ImprovementImportance.html.

APA

Wolfram 语言. (2012). ImprovementImportance. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/ImprovementImportance.html 年

BibTeX

@misc{reference.wolfram_2024_improvementimportance, author="Wolfram Research", title="{ImprovementImportance}", year="2012", howpublished="\url{https://reference.wolfram.com/language/ref/ImprovementImportance.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_improvementimportance, organization={Wolfram Research}, title={ImprovementImportance}, year={2012}, url={https://reference.wolfram.com/language/ref/ImprovementImportance.html}, note=[Accessed: 21-November-2024 ]}