IncludeSingularSolutions
is an option for DSolve that specifies whether singular solutions should be returned along with the general solution for a nonlinear ordinary differential equation.
Details
- Singular solutions are also known as envelope solutions or equilibrium solutions.
- Singular solutions cannot be obtained by assigning finite numerical values to the arbitrary constants in the general solution for a nonlinear differential equation. Instead, they can be obtained by constructing the envelope of the family of curves represented by the general solution.
- For example, if the general solution of a first-order ODE is given by the equation
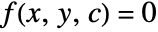, where 
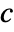is an arbitrary constant, then the singular solutions can be obtained by solving the envelope equations 
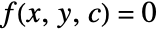and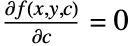 
. - The following illustration shows the singular solution (envelope) for a nonlinear ODE whose general solution is a family of straight lines.
- Singular solutions are closely related to physical phenomena such as caustics and wavefronts in optics that can be explained using envelope constructions.
- Possible settings for IncludeSingularSolutions are:
-
False return only general solutions depending on constants C[i] True return both general and singular solutions
Examples
open allclose allBasic Examples (2)
By default, DSolve returns the general solution for this ODE:
Use IncludeSingularSolutions to compute singular solutions along with the general solution:
Visualize the general solution along with the envelope formed by this family:
Find the general solution of a logistic equation:
The singular solutions in this case are the "equilibrium" solutions y=0 and y=1:
Visualize the general solution along with the equilibrium solutions:
Properties & Relations (1)
Obtain the general solution of a nonlinear ODE:
Construct the envelope for the family of curves defined by the general solution:
Obtain the same result using IncludeSingularSolutions:
Visualize the general solution along with the envelope formed by this family:
Text
Wolfram Research (2022), IncludeSingularSolutions, Wolfram Language function, https://reference.wolfram.com/language/ref/IncludeSingularSolutions.html.
CMS
Wolfram Language. 2022. "IncludeSingularSolutions." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/IncludeSingularSolutions.html.
APA
Wolfram Language. (2022). IncludeSingularSolutions. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/IncludeSingularSolutions.html