InscribedBall

InscribedBall[{p1,p2,…}]

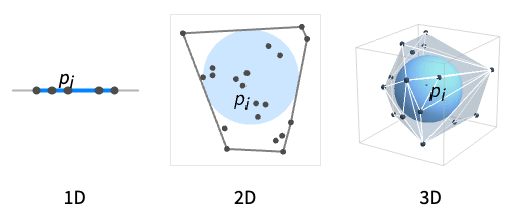
点 p1,p2,…の凸包内の最大の球を与える．

詳細

  • InscribedBallは，プラグゲージ円あるいは最大内接円としても知られている．
  • InscribedBallは，点の集合の凸包に内接する最大測度（円弧，長さ，面積等）のBallを与える．

例題

すべて開くすべて閉じる

例  (2)

点からの2Dの内接球：

この領域は，点の凸包内に存在する最大の球である：

点からの3D内接球：

この領域は，点の凸包内に存在する最大の球である：

スコープ  (1)

点の集合から1D内接球を作成する：

2D内接球：

3D内接球：

アプリケーション  (1)

ボロノイ(Voronoi)メッシュ内の内接球：

特性と関係  (3)

InscribedBallは点の凸包内に存在する最大のBallである：

CircumscribedBallを使って点を包み込む最小のBallを得る：

Insphereを使って点で定義されるシンプレックスに内接できるSphereを得る：

Wolfram Research (2023), InscribedBall, Wolfram言語関数， https://reference.wolfram.com/language/ref/InscribedBall.html.

テキスト

Wolfram Research (2023), InscribedBall, Wolfram言語関数， https://reference.wolfram.com/language/ref/InscribedBall.html.

CMS

Wolfram Language. 2023. "InscribedBall." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/InscribedBall.html.

APA

Wolfram Language. (2023). InscribedBall. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/InscribedBall.html

BibTeX

@misc{reference.wolfram_2024_inscribedball, author="Wolfram Research", title="{InscribedBall}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/InscribedBall.html}", note=[Accessed: 05-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_inscribedball, organization={Wolfram Research}, title={InscribedBall}, year={2023}, url={https://reference.wolfram.com/language/ref/InscribedBall.html}, note=[Accessed: 05-November-2024 ]}