CircumscribedBall[{p1,p2,…}]
gives a ball with minimal radius that encloses the points p1, p2, ….


CircumscribedBall
CircumscribedBall[{p1,p2,…}]
gives a ball with minimal radius that encloses the points p1, p2, ….
Details
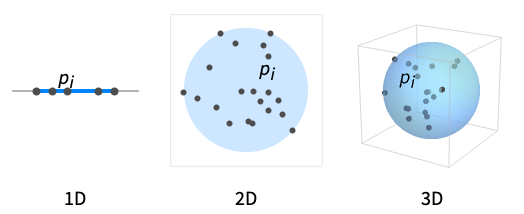
- CircumscribedBall is also known as minimal enclosing circle.
- CircumscribedBall gives the Ball of smallest measure (arc length, area, …) that contains all the points pi.
Examples
open all close allBasic Examples (2)
Scope (1)
Properties & Relations (3)
CircumscribedBall is the smallest Ball that encloses the points:
Use InscribedBall to get a largest Ball that lies inside the convex hull of points:
Use Circumsphere to get the Sphere that circumscribes the points:
See Also
Related Guides
History
Text
Wolfram Research (2023), CircumscribedBall, Wolfram Language function, https://reference.wolfram.com/language/ref/CircumscribedBall.html.
CMS
Wolfram Language. 2023. "CircumscribedBall." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/CircumscribedBall.html.
APA
Wolfram Language. (2023). CircumscribedBall. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/CircumscribedBall.html
BibTeX
@misc{reference.wolfram_2025_circumscribedball, author="Wolfram Research", title="{CircumscribedBall}", year="2023", howpublished="\url{https://reference.wolfram.com/language/ref/CircumscribedBall.html}", note=[Accessed: 09-January-2026]}
BibLaTeX
@online{reference.wolfram_2025_circumscribedball, organization={Wolfram Research}, title={CircumscribedBall}, year={2023}, url={https://reference.wolfram.com/language/ref/CircumscribedBall.html}, note=[Accessed: 09-January-2026]}