Insphere

Insphere[{p1,…,pn+1}]

内の点 piで定義されるシンプレックス（三角形，四面体等）に内接する最大の球を返す．

Insphere[poly]

多角形または多面体 poly の内接球を与える．

詳細

  • Insphereは，内接円あるいは内接円板としても知られている．
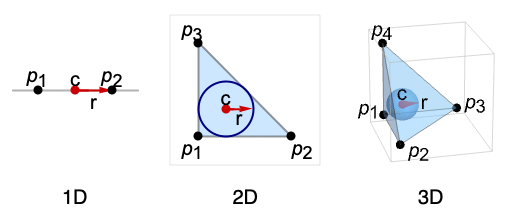
  • Insphereは，点 piで定義されたシンプレックス（三角形，四面体等）に内接する（弧長，面積等が）最大の Sphereを与える．
  • Insphereを評価するとSphere[c,r]になる．ただし，中心 c は内心として知られ，半径 r は関連付けられたシンプレックスの内接円の半径として知られる．
  • Insphere は 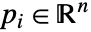について定義され，アフィン独立である．
  • 多面体については，Insphere[poly]は，多面体 poly に包含され，多面体の各面に接する球を返す．
  • 多角形については，Insphere[poly]は，多角形 poly に包含され多角形の各辺に接する球を返す．
  • Insphereは，GeometricSceneの記号の点と一緒に使うことができる．

例題

すべて開くすべて閉じる

例  (2)

2Dにおける内接円：

3Dにおける：

正八面体の内接球：

その表面積：

スコープ  (17)

グラフィックス  (6)

指定  (2)

異なる次元の内接球：

Insphereを評価するとSphereになる：

中心と半径を求める：

スタイリング  (4)

彩色された外接球：

FaceFormを使って表面と裏面に異なる特性を指定することができる：

さまざまな鏡面反射指数の外接球：

赤く輝く黒い外接球：

Opacityは表面の不透明度を指定する：

領域  (11)

Insphereは任意数の次元で使うことができる：

外心と外接半径を得る：

埋込み次元は球がある空間の次元である：

幾何次元は形それ自体の次元である：

帰属判定：

帰属条件を得る：

面積：

重心：

点からの距離：

これをプロットする：

点からの符号付き距離：

これをプロットする：

領域内の最近点：

包み込んでいる球までの最近点：

球は有界である：

その範囲を求める：

Insphere上でIntegrateする：

その上で最適化する：

Insphere上で方程式を解く：

アプリケーション  (3)

内接三角形と円板を再帰的に構築する：

Insphereを使って三角形分割された領域の円充填を生成する．まず，領域の三角形分割を行う：

Insphereを使って各三角形の円を求める：

充填密度を計算する：

Insphereを使って三角形分割された領域の球充填を求める．まず，領域を離散化し，三角形分割を行う：

Insphereを使って各四面体についての球を計算する：

充填密度を計算する：

特性と関係  (2)

Insphereは，Simplexに内接する最大のSphereである：

3Dで：

Circumsphereを使ってSimplexに外接するSphere（青）を得る：

3Dで：

おもしろい例題  (1)

ランダムな内接球の集合：

Wolfram Research (2015), Insphere, Wolfram言語関数， https://reference.wolfram.com/language/ref/Insphere.html （2019年に更新）.

テキスト

Wolfram Research (2015), Insphere, Wolfram言語関数， https://reference.wolfram.com/language/ref/Insphere.html （2019年に更新）.

CMS

Wolfram Language. 2015. "Insphere." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2019. https://reference.wolfram.com/language/ref/Insphere.html.

APA

Wolfram Language. (2015). Insphere. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Insphere.html

BibTeX

@misc{reference.wolfram_2024_insphere, author="Wolfram Research", title="{Insphere}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/Insphere.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_insphere, organization={Wolfram Research}, title={Insphere}, year={2019}, url={https://reference.wolfram.com/language/ref/Insphere.html}, note=[Accessed: 21-November-2024 ]}