Insphere

Insphere[{p1,…,pn+1}]

给出内切于由 中点 pi 定义的单形的球.

Insphere[poly]

给出多面体或多边形 poly 的内圆.

更多信息

  • Insphere 也被称为内切圆、内接圆或内切圆盘.
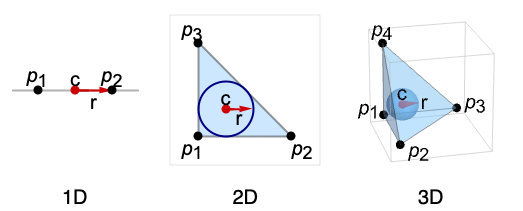
  • Insphere 给出可以内切由点 pi 定义的单形（三角形、四面体）的最大度量（弧长、面积等）的 Sphere.
  • Insphere 计算结果为 Sphere[c,r]，其中中心 c 被称为内心，半径 r 被称为相应单纯形的内径.
  • Insphere 对于 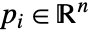有定义，并且仿射无关.
  • 对于多面体，Insphere[poly] 返回包含在多面体 poly 内并正切于每个多面体面的球.
  • 对于多边形，Insphere[poly] 返回包含在多边形 poly 内并正切于每个多边形边的球.
  • Insphere 可与 GeometricScene 中的符号点一起使用.

范例

打开所有单元关闭所有单元

基本范例  (2)

二维空间中的内切圆：

三维空间中：

正则八面体的内切圆：

表面积：

范围  (17)

图形  (6)

规范  (2)

不同维度的的内切球：

Insphere 计算结果为 Sphere：

得到圆心和半径：

样式  (4)

彩色的内切球：

利用 FaceForm 可以指定正面和背面的不同属性：

具有不同镜面反射指数的内切球：

发红光的黑色内切球：

Opacity 指定了表面不透明度：

区域  (11)

Insphere 适用于任意维度：

获取内心和内径：

嵌入维度是球所在空间的维度：

几何维度是形状自身的维度：

成员性检验：

获取成员条件：

面积：

形心：

到某点的距离：

绘图：

到某点的带符号距离：

绘图：

区域的最近点：

到一个封闭球面的最近点：

球是有界的：

求它的范围：

在 Insphere 上进行 Integrate：

在内切球上面进行优化：

在 Insphere 上解方程：

应用  (3)

递归地构建内接三角形和内切圆：

使用 Insphere 生成对三角化区域填充的圆. 首先对区域进行三角化:

使用 Insphere 计算每个三角形对应的圆：

计算填充密度：

使用 Insphere 生成对三角化区域填充的球. 首先对区域进行离散和三角化：

使用 Insphere 计算每个四面体对应的球：

计算填充密度：

属性和关系  (2)

Insphere 是可以内切于 Simplex 中的最大 Sphere：

在三维空间中：

使用 Circumsphere 得到外接于 Simplex 的 Sphere（蓝色）：

在三维空间中：

巧妙范例  (1)

随机内切圆的组合：

Wolfram Research (2015)，Insphere，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Insphere.html （更新于 2019 年）.

文本

Wolfram Research (2015)，Insphere，Wolfram 语言函数，https://reference.wolfram.com/language/ref/Insphere.html （更新于 2019 年）.

CMS

Wolfram 语言. 2015. "Insphere." Wolfram 语言与系统参考资料中心. Wolfram Research. 最新版本 2019. https://reference.wolfram.com/language/ref/Insphere.html.

APA

Wolfram 语言. (2015). Insphere. Wolfram 语言与系统参考资料中心. 追溯自 https://reference.wolfram.com/language/ref/Insphere.html 年

BibTeX

@misc{reference.wolfram_2024_insphere, author="Wolfram Research", title="{Insphere}", year="2019", howpublished="\url{https://reference.wolfram.com/language/ref/Insphere.html}", note=[Accessed: 21-November-2024 ]}

BibLaTeX

@online{reference.wolfram_2024_insphere, organization={Wolfram Research}, title={Insphere}, year={2019}, url={https://reference.wolfram.com/language/ref/Insphere.html}, note=[Accessed: 21-November-2024 ]}